在边长为1的正方形网格中,有△ABC和半径为2的⊙P.
以点M为位似中心,在网格中将△ABC放大2倍得到△A´B´C´,请画出△A´B´C´;

在(1)所画的图形中,求线段AB的对应线段A´B´被⊙P所截得的弦DE的长.
如图(14),已知  ,
, ,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
求C点坐标及直线BC的解析式;
一抛物线经过B、C两点,且顶点落在x轴正半轴上,求该抛物线的解析式并画出函数图象;
现将直线BC绕B点旋转与抛物线相交于另一点P,请找出抛物线上所有满足到直线AB距离为
 的点P.
的点P.
作图题
在方格纸中,每个小格的顶点叫做格点,以格点连线为边三角形叫做格点三角形.图中的每个小正方形的边长都是1个单位.请你在图中,画出两个相似但不全等的格点
钝角三角形.
如图,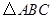 在方格纸中
在方格纸中
(1)请在方格纸上建立平面直角坐标系,使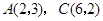 ,并求出
,并求出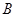 点坐标;
点坐标;
(2)以原点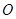 为位似中心,相似比为2,在第一象限内将
为位似中心,相似比为2,在第一象限内将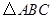 放大,画出放大后的图形
放大,画出放大后的图形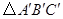 ;
;
(3)计算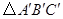 的面积
的面积 .
.
(本题6分)已知格点△ABC.
(1)画出与△ABC相似的格点△A1B1C1,使△A1B1C1与△ABC的相似比为2;
(2)画出与△ABC相似的格点△A2B2C2,使△A2B2C2与△ABC的相似比为 ;
;
(3)格点△A1B1C1和格点△A2B2C2的相似比为 .
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.求证:∠DAF=∠CDE
问△ADF与△DEC相似吗?为什么?
若AB=4,AD=3
 ,AE=3,求AF的长.
,AE=3,求AF的长.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;先作△ABC关于直线
 成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
成轴对称的图形,再向上平移1个单位,得到△A1B1C1;以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.

如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)试说明△ACB∽△DCE;
(2)请判断EF与AB的位置关系并说明理由.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)将△ABC向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.
⑴以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2
⑵连接⑴中的AA′,求四边形AA′C′C的周长.
(结果保留根号)
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)先作△ABC关于直线 成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
如图所示,已知:⊿ABC∽⊿DAC,AD=2,AC=4,BC=6,∠B=36°,∠D=117°,
(1)求AB的长;
(2)求CD的长;
(3)求∠BAD的大小。
试题篮
()