在△ABC中,AE∶EB="1" ∶2,EF∥BC,AD∥BC交CE的延长线于D,求S△AEF∶S△BCE的值.
在ΔABC中,BA=BC=20cm ,AC=3
,AC=3 0cm,点P从A点出发,沿着AB
0cm,点P从A点出发,沿着AB 以每秒4c
以每秒4c m的速度向B点运动;同时点Q从C点出发,沿CA
m的速度向B点运动;同时点Q从C点出发,沿CA 以每秒3cm的速度向A点运动,设运动时间为x.
以每秒3cm的速度向A点运动,设运动时间为x.

(1)当x为何值时,P Q∥BC?
Q∥BC?
(2)当 ,求
,求 的值;
的值;
.已知:如图,∠ABE=90°,且AB=BC=CD=DE,请认真研究图形与所给条件,然后回答:图中是否存在相似的三角形?若存在,请加以说明;若不存在,请说明理由.
.如图,是利用木杆撬石头的示意图.现有一块石头,要使其滚动,杠杆的B端必须向上翘起12cm,已知杠杆的动力臂OA与阻力臂OB之比为5:1,求要使这块石头滚动,至少要将杠杆A端下压多少厘米.
如图,已知△ABC中,AC=10 ,AB=16,问在AB边上是否存在这样的点P,使△APC∽△ACB,若存在,求AP的长;若不存在,请说明理由.
,AB=16,问在AB边上是否存在这样的点P,使△APC∽△ACB,若存在,求AP的长;若不存在,请说明理由.
如图所示,矩形ABCD中,AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、MN、FN,过ΔFMN三边的中点作ΔPQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题: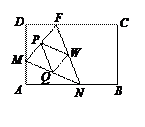
(1)说明ΔFMN∽ΔQWP;
(2)设0≤x≤4.试问x为何值时,ΔPQW为直角三角形?
(3)试用含的代数式表示MN2,并求当x为何值时,MN2最小?求此时MN2的值.
如图,路边有一根电线杆AB和一块半圆形广告牌,在太阳光照射下,杆顶A的影子刚好落在半圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在平地上一点E,若BC=5米,半圆形的广告牌直径为6米,DE=2米.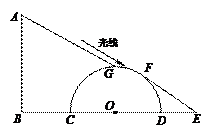
(1)求电线杆落在广告牌上的影子长(即︵CG的长).
(2)求电线杆的高度.
如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并说明你的理由;
(2)若AB=,BC=2,求⊙O的半径.
如图,已知∆ABC中,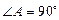 ,
, ,D是AB上一动点,DE∥BC,交AC于E,将四边形BDEC沿DE向上翻折,得四边形
,D是AB上一动点,DE∥BC,交AC于E,将四边形BDEC沿DE向上翻折,得四边形 ,
, 与AB、AC分别交于点M、N.
与AB、AC分别交于点M、N.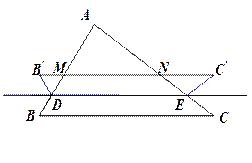
(1)证明:∆ADE 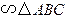 ;
;
(2)设AD为x,梯形MDEN的面积为y,试求y与x的函数关系式. 当x为何值时y有最大值?
已知:在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.如图甲,当AC=BC,且CE=EA时,则有EF=EG;
(1)如图乙①,当AC=2BC,且CE=EA时,则线段EF与EG的数量关系是:EF EG;
(2)如图乙②,当AC=2BC,且CE=2EA时,请探究线段EF与EG的数量关系,并证明你的结论;
(3)当AC=mBC,且CE=nEA时,请探究线段EF与EG的数量关系,直接写出你的结论(不必证明).
如图,在△ABC中,∠A=90°,AB=8,AC=6,M是AB上的动点(不与A、B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O中作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在点M的运动过程中,设△MNP与梯形BCNM重合的面积为y,求y关于x的函数关系式,并求x为何值时,y的值最大,最大值是多少?
如图,在矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:ΔABE∽ΔDFA;
(2)若AB=6,AD=12,BE=8,求DF的长
如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
试题篮
()