初中数学相似多边形的性质解答题

如图，在中，，是斜边上的中线，，，点是延长线上的一动点，过点作，交延长线于点，
设．

（1）求关于的函数关系式及定义域；
（2）联结，当平分时，求的长；
（3）过点作交于，当和相似时，求的值．

如图，的顶点A、B在二次函数的图像上，又点A、B[来分别在轴和轴上，∠ABO＝．

（1）求此二次函数的解析式；

（2）过点作∥交上述函数图像于点，

点 在上述函数图像上，当 与 相似时，求点 的坐标．

（本题满分12分）
如图，梯形中，∥，，点在边上，与相交于点，且．

求证：（1）∽；   
（2）．

如图，在中，点在边上，点在边上，且∥，．

（1）求证：∥；
（2）如果，，求的值．

如图，□中，∥，∥，点是的中点，和相交于点．

（1）求的值；
（2）如果，，请用、表示   

（本题满分14分，其中第（1）、（2）小题各4分，第（3）小题6分）已知：如图，在平面直角坐标系xOy中，二次函数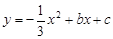的图像经过点A（-1,1）和点B（2,2），该函数图像的对称轴与直线OA、OB分别交于点C和点D．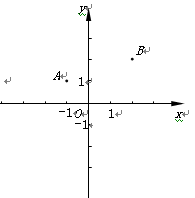

（1）求这个二次函数的解析式和它的对称轴；
（2）求证：∠ABO=∠CBO；
（3）如果点P在直线AB上，且△POB
与△BCD相似，求点P的坐标．

（本题满分12分，其中第（1）小题5分，第（2）小题7分）
已知：如图，在△ABC中，AD是边BC上的中线，点E在线段BD上，且BE=ED，过点B作BF∥AC，交线段AE的延长线于点F．

（1）求证：AC=3BF；
（2）如果，求证：．

已知：如图，矩形DEFG的一边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上，AH是边BC上的高，AH与GF相交于点K，已知BC=12，AH=6，EF∶GF=1∶2，求矩形DEFG的周长．

在Rt△ABC中，∠ACB=90，AC=BC，CD⊥AB于点D，点E为AC边上一点，联结BE交CD于点F，过点E作EG⊥BE交AB于点G，
如图1，当点E为AC中点时，线段EF与EG的数量关系是        ；
如图2，当，探究线段EF与EG的数量关系并且证明；
如图3，当，线段EF与EG的数量关系是        ．

如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，以AB上一点O为圆心，AD为弦作⊙O．
（1）求证：BC为⊙O的切线；  
(2）若AC= 6，tanB=，求⊙O的半径．

如图1，在△ABC中，∠ACB=90°，AC=3，BC=4，将△ABC绕顶点C顺时针旋转30°，得到△A′B′C．联结A′A、B′B，设△ACA′和△BCB′的面积分别为S_△ACA′ 和S_△BCB′．

（1）直接写出S_△ACA′ ︰S_△BCB′ 的值                  ；
（2）如图2，当旋转角为（0°＜＜180°）时，S_△ACA′ 与S_△BCB′ 的比值是否发生变化，若不变请证明；若改变，写出变化后的比值（可用含的代数式表示）．

如图，在△ABC中，，点在上，为⊙的直径，
⊙切于，若，求⊙的半径．

（本小题8分）如图，AB为⊙O的直径，割线PCD交⊙O于C、D, .

（1）求证：PA是⊙O的切线；
（2）若PA=6，CD=3PC，求PD的长.

已知：如图，正方形ABCD的边长为a，BM，DN分别平分正方形的两个外角，且满足
，连结MC，NC，MN．

（1）填空：与△ABM相似的三角形是△       ，=        ；（用含a的代数式表示）
（2）求的度数；
（3）猜想线段BM，DN和MN之间的等量关系并证明你的结论．

已知：如图，在菱形ABCD中，E为BC边上一点，∠AED=∠B．

（1）求证：△ABE∽△DEA；
（2）若AB=4，求的值．