初中数学相似多边形的性质解答题

(本题满分12分)已知AB是⊙O的一条弦，CD是⊙O的直径，CD⊥AB，垂足为K．现取一块三角板，把它的一个锐角顶点固定在点C处，该锐角的两边(从左到右)与直线AB和圆分别相交于E、F和G、H．

(1) 若∠C的一边过圆心，请选择图10-1或图10-2所示，求证： △CEF∽△CHG；
(2) 若∠C的边不过圆心，在图10-3中补全一种示意图，请你观察所画的图形，并判断(1)中的结论是否仍然成立？若成立，给予证明；若不成立，请说明理由．

(本题满分12分)
如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．

(1) 填空：∠ABC＝___________°，BC＝_________；
(2) 判断△ABC与△DEF是否相似，并证明你的结论．

如图，在矩形ABCD中，AB=3cm，AD=4cm，点E是BC上一动点（不与B、C重合），且DF⊥AE，垂足为F. 设AE=xcm，DF=ycm.

求证：△DFA∽△ABE；
试求y与x之间的函数关系式，并求出自变量的取值范围.

如图，平行四边形ABCD中，AB＝5，BC＝10，BC边上的高AM=4，E为 BC边上的一个动点（不与B、C重合）．过E作直线AB的垂线，垂足为F． FE与DC的延长线相交于点G，连结DE，DF．.

求证：ΔBEF ∽ΔCEG．
当点E在线段BC上运动时，△BEF和△CEG的周长之间有什么关系？并说明你的理由．
设BE＝x，△DEF的面积为 y，请你求出y和x之间的函数关系式，并求出当x为何值时,y有最大值，最大值是多少？

如图，在Rt△ABC中，∠ACB=90º，AB=10，AC=6，点E、F分别是边AC、BC上的动点，过点E作ED⊥AB于点D，过点F作FG⊥AB于点G，DG的长始终为2．
（1）当AD=3时，求DE的长；
（2）当点E、F在边AC、BC上移动时，设，，
求关于的函数解析式，并写出函数的定义域；
（3）在点E、F移动过程中，△AED与△CEF能否相似，
若能，求AD的长；若不能，请说明理由．

（本小题满分12分）
如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=EF=9，∠BAC＝∠DEF＝90°，固定△ABC，将△EFD绕点A 顺时针旋转，当DF边与AB边重合时，旋转中止。不考虑旋转开始和结束时重合的情况，设DE、DF（或它们的延长线）分别交BC（或它的延长线）于G、H点，如图（2）。

（1）问：始终与△AGC相似的三角形有       及       ；
（2）设CG＝x，BH＝y，求y关于x的函数关系式（只要求根据2的情况说明理由）；
（3）问：当x为何值时，△AGH是等腰三角形？

（本小题满分12分）某班同学到野外活动，为测量一池塘两端A、B的距离，设计了几种方案，下面介绍两种：（I）如图（1），先在平地取一个可以直接到达A、B的点C，并分别延长AC到D，BC到E，使DC=AC，BC=EC，最后测出DE的距离即为AB的长。（II）如图（2），先过B点作AB的垂线BF，再在BF上取C、D两点，使BC=CD，接着过点D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离。阅读后回答下列问题：

（1）方案（I）是否可行？为什么？
（2）方案（II）是否切实可行？为什么？
（3）方案（II）中作BF⊥AB，ED⊥BF的目的是           ；若仅满足∠ABD=∠BDE≠90°，方案（II）是否成立？
（4）方案（II）中，若使BC=n·CD，能否测得（或求出）AB的长？理由是        ，若ED=m，则AB=     。

（本小题满分8分）在直角坐标系中，已知点A（－2，0）、B（0，4）、C（0，3），过点C作直线交x轴于点D，使得以   D、O、C为顶点的三角形与△AOB相似，求点D的坐标。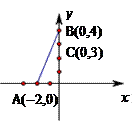

（本小题满分6分）如图，在△ABC和△ADE中，∠BAD=∠CAE，∠ABC=∠ADE。

（1）写出图中两对相似三角形（不得添加辅助线）；
（2）请分别说明两对三角形相似的理由。

如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21。动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动。设运动的时间为t（秒）．
设△BPQ的面积为S，求S与t之间的函数关系式
当线段PQ与线段AB相交于点O，且2AO＝OB时，求t的值．
当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？
是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由．

为了测量学校操场上旗杆的高度，小明请同学帮忙，测量了同一时刻自己的影长EC和旗杆的影长BC分别为0.6m和3.6m，如图，如果小身高CD为1.5m，请计算旗杆AB的高度。

如图，⊿ABC在平面直角坐标系内三顶点坐标分别为
先画出⊿ABC；
以B为位似中心，画出⊿A₁B₁C₁，使⊿A₁B₁C₁与⊿ABC相似且相似比为2:1

如图，在直角梯形ABCD中，AB∥DC，∠D = 90^o，AC⊥BC，
AB =" 10cm" , BC = 6cm，F点以2 cm／秒的速度在线段AB上由A向B匀速运动， E点同时以1 cm／秒的速度在线段BC上由B向C匀速运动，设运动时间为 t 秒 ( 0 < t < 5 )．

（1）求证：△ A C D ∽△ B A C ；
（2）求DC的长；
（3）设四边形AFEC的面积为 y ，求 y关于t的函数关系式．

在平面直角坐标系xOy中,反比例函数的图象与抛物线 
交于点A(3, n).
（1）求n的值及抛物线的解析式；
（2） 过点A作直线BC，交x轴于点B，交反比例函数（）的图象于点C，且AC=2AB，求B、C两点的坐标；                              
（3）在（2）的条件下，若点P是抛物线对称轴上的一点，且点P到x轴和直线BC的距离相等，求点P的坐标.

(本小题满分5分)
已知：如图，在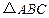中，D是AC上一点，联结BD，且∠ABD =∠ACB.

（1）求证：△ABD∽△ACB；
（2）若AD=5，AB= 7，求AC的长.