初中数学相似多边形的性质解答题

在Rt△ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP=．
（1）如图，当点E在边AC上时，点E不与点A、C重合，

①求证：△AEP∽△ABC
②设AP=x，求MP的长 （用含x的代数式表示）
（2）若△AME∽△ENB，求AP的长．

如图，Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的，连结CC′交斜边于点E，CC′的延长线交BB′于点F。

（1）若AC=3，AB=4，求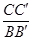
（2）证明：△ACE∽△FBE；
（3）设∠ABC=，∠CAC′=，试探索、满足什么关系时，△ACE与△FBE是全等三角形，并说明理由。

已知矩形纸片ABCD中，AB＝2，BC＝3．
操作：将矩形纸片沿EF折叠，使点B落在边CD上．
探究：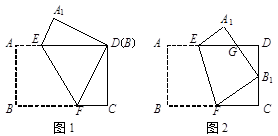

（1）如图1，若点B与点D重合，你认为△EDA₁和△FDC全等吗？如果全等，请给出证明，如果不全等，请说明理由；
（2）如图2，若点B与CD的中点重合，请你判断△FCB₁、△B₁DG和△EA₁G之间的关系，如果全等，只需写出结果，如果相似，请写出结果，求出相应的相似比；
（3）如图2，请你探索，当点B落在CD边上何处，即B₁C的长度为多少时，△FCB₁与△B₁DG全等．

（本小题10分）如图，已知在中，是平分线，点在边上，且．

求证：（1）∽；（2）.

已知：把和按如图（1）摆放（点与点重合），点、（）、在同一条直线上．，，，，．如图（2），从图（1）的位置出发，以的速度沿向匀速移动，在移动的同时，点从的顶点出发，以2 cm/s的速度沿向点匀速移动.当的顶点移动到边上时，停止移动，点也随之停止移动．与相交于点，连接，设移动时间为．

（1）当为何值时，点在线段的垂直平分线上？
（2）连接，设四边形的面积为，求与之间的函数关系式；是否存在某一时刻，使面积最小？若存在，求出的最小值；若不存在，说明理由．
（3）是否存在某一时刻，使、、三点在同一条直线上？若存在，求出此时的值；若不存在，说明理由．（图（3）供同学们做题使用）

如图，在等边中，于点，点在边上运动，过点作与边交于点，连结，以为邻边作□，设□与重叠部分图形的面积为，线段的长为

（1）求线段的长（用含的代数式表示）；
（2）当四边形为菱形时，求的值；
（3）求与之间的函数关系式；
（4）设点关于直线的对称点为点，当线段的垂直平分线与直线相交时，设其交点为，当点与点位于直线同侧（不包括点在直线上）时，直接写出的取值范围．

如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB_l∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB₁于F，G是EF中点，连结DG．设点D运动的时间为t秒．

（1）当t为何值时，AD=AB，并求出此时DE的长度；
（2）当△DEG与△ACB相似时，求t的值；
（3）以DH所在直线为对称轴，线段AC经轴对称变换后的图形为A′C′．当t>时，连结C ′C，则以CC´为直径的圆何时与直线AB相切？

在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．
（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；
（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：；
（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．

如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．

（1）若△BPQ与△ABC相似，求t的值；
（2）连接AQ、CP，若AQ⊥CP，求t的值．

以平面上一点O为直角顶点，分别画出两个直角三角形，记作△AOB和△COD，其中∠ABO=∠DCO=30°．
（1）点E、F、M分别是AC、CD、DB的中点，连接FM、EM．

①如图1，当点D、C分别在AO、BO的延长线上时，=_______；

②如图2，将图1中的△AOB绕点O沿顺时针方向旋转角（），其他条件不变，判断的值是否发生变化，并对你的结论进行证明；

（2）如图3，若BO=，点N在线段OD上，且NO="2." 点P是线段AB上的一个动点，在将△AOB绕点O旋转的过程中，线段PN长度的最小值为_______，最大值为_______．

如图，▱ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x²-7x+12=0的两个根，且OA＞OB．

（1）求sin∠ABC的值；
（2）若E为x轴上的点，且S_△AOE=，求经过D、E两点的直线的解析式，并判断△AOE与△DAO是否相似？
（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由．

如图，点A是x轴正半轴上的动点，点B的坐标为（0，4），将线段AB的中点绕点A按顺时针方向旋转90°得点C，过点C作x轴的垂线，垂足为F，过点B作y轴的垂线与直线CF相交于点E，点D是点A关于直线CF的对称点，连接AC、BC、CD，设点A的横坐标为t．
（Ⅰ）线段AB与AC的数量关系是              ，位置关系是              ．
（Ⅱ）当t=2时，求CF的长；
（Ⅲ）当t为何值时，点C落在线段BD上？求出此时点C的坐标；
（Ⅳ）设△BCE的面积为S，求S与t之间的函数关系式．

如图，矩形ABCD中，AB="10" cm，BC="6" cm．现有两个动点P，Q分别从A，B同时出发，点P在线段AB上沿AB方向作匀速运动，点Q在线段BC上沿BC方向作匀速运动，已知点P的运动速度为1 cm/s，运动时间为t s．

（1）设点Q的运动速度为 cm/s．
①当△DPQ的面积最小时，求t的值；
②当△DAP∽△QBP相似时，求t的值．
（2）设点Q的运动速度为a cm/s，问是否存在a的值，使得△DAP与△PBQ和△QCD这两个三角形都相似？若存在，请求出a的值；若不存在，请说明理由．

已知：把和按如图（1）摆放（点与点重合），点、（）、在同一条直线上．，，，，．如图（2），从图（1）的位置出发，以的速度沿向匀速移动，在移动的同时，点从的顶点出发，以2 cm/s的速度沿向点匀速移动.当的顶点移动到边上时，停止移动，点也随之停止移动．与相交于点，连接，设移动时间为．

（1）当为何值时，点在线段的垂直平分线上？
（2）连接，设四边形的面积为，求与之间的函数关系式；是否存在某一时刻，使面积最小？若存在，求出的最小值；若不存在，说明理由．
（3）是否存在某一时刻，使、、三点在同一条直线上？若存在，求出此时的值；若不存在，说明理由．（图（3）供同学们做题使用）

在Rt△ABC中，∠A=90°，AB=6，AC=8，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上一动点，点Q为边AC上一动点，且∠PDQ=90°．

（1）求ED、EC的长；
（2）若BP=2，求CQ的长；
（3）记线段PQ与线段DE的交点为点F，若△PDF为等腰三角形，求BP的长．