初中数学相似多边形的性质解答题

如图，在平面直角系中，点A、B分别在x轴、y轴上，A（8，0），B（0，6），点P从点B出发，沿BA以每秒1个单位的速度向点A运动，点Q从点A出发，沿AO以每秒1个单位的速度向点O运动，当点Q到达点O时，两点同时停止运动，设点Q的运动时间为t秒．

（1）用含t的代数式表示C点坐标；
（2）如图1，连接PQ，过点Q作QC⊥AO交AB于点C，在整个运动过程中，当t为何值时，△CPQ为等腰三角形？
（3）如图2，以QC为直径作⊙D，⊙D与AB的另一个公共点为E．问是否存在某一时刻t，使得以BC、CE、AE的长为边的三角形为直角三角形？若存在，直接写出一个符合题意的t的值；若不存在，请说明理由．

(本题满分10分)
如图，在平面直角坐标系中，直线AB：分别与x轴、y轴交于点A、B，.

（1）求b的值.
（2）动点C从A点出发以2个单位/秒的速度沿x轴的正半轴运动，动点D从B点出发以1个单位/秒的速度沿y轴的正半轴运动.运动时间为t（t＞0），过A作x轴的垂线交直线CD于点P，过P作y轴的垂线交直线AB于点F，设线段BF的长为d(d＞0)，求d与t的函数关系式.
（3）在（2）的条件下，以点A为圆心，2为半径作⊙A，过点C作不经过第三象限的直线l与⊙A相切，切点为Q, 直线l与y轴交于点E，作QH⊥AE于H，交x轴于点G，是否存在t值，使,若存在，求出t值；若不存在，请说明理由.

如图1，小红将一张直角梯形纸片沿虚线剪开，得到矩形和三角形两张纸片，测得AB=15，AD=12．在进行如下操作时遇到了下面的几个问题，请你帮助解决．

（1）将△EFG的顶点G移到矩形的顶点B处，再将三角形绕点B顺时针旋转使E点落在CD边上，此时EF恰好经过点A（如图2），求FB的长度．
（2）在（1）的条件下，小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4，请问哪种包裹纸片的方法使得未包裹住的面积大？（纸片厚度忽略不计）请你通过计算说服小红．

如图，在平面直角坐标系中，矩形AOBC的边长为AO=6，

（1）如图①，E是OB的中点，将△AOE沿AE折叠后得到△AFE，点F在矩形AOBC内部，延长AF交BC于点G．求点G的坐标；
（2）定义：若以不在同一直线上的三点中的一点为圆心的圆恰好过另外两个点，这样的圆叫做黄金圆．如图②，动点P以每秒2个单位的速度由点C向点A沿线段CA运动，同时点Q以每秒4个单位的速度由点O向点C沿线段OC运动,求当 P、Q、C三点恰好构成黄金圆时点P的坐标．

如图，∠C=90°，点A、B在∠C的两边上，CA=30，CB=20，连结AB．点
P从点B出发，以每秒4个单位长度的速度沿BC方向运动，到点C停止．当点P与B、C两点不重合时，作PD⊥BC交AB于D，作DE⊥AC于E．F为射线CB上一点，且∠CEF=∠ABC．设点P的运动时间为x（秒）．

（1）用含有x的代数式表示CE的长；
（2）求点F与点B重合时x的值；
（3）当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y（平方单位）．求y与x之间的函数关系式；
（4）当x为某个值时，沿PD将以D、E、F、B为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的x值．

如图，直线l经过点A（1，0），且与双曲线y＝（x＞0）交于点B（2，1），过点P（p，p－1）（p＞1）作x轴的平行线分别交曲线y＝（x＞0）和y＝－（x＜0）于M，N两点．

（1）求m的值及直线l的解析式；
（2）若点P在直线y＝2上，求证：△PMB∽△PNA；
（3）是否存在实数p，使得S_△AMN＝4S_△APM？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．

如图，在平面直角坐标系中，点A、B的坐标分别为（-5，0）和（5，0），以AB为直径在x轴的上方作半圆O，点C是该半圆上第一象限内的一个动点，连结AC、BC，并延长BC至点D，使BC=CD，过点D作x轴的垂线，分别交x轴、线段AC于点E、F，E为垂足，连结OF．

（1）当∠CAB=30°时，求弧BC的长；
（2）当AE=6时，求弦BC的长；
（3）在点C运动的过程中，是否存在以点O、E、F为顶点的三角形与△DEB相似？若存在，请求出此时E点的坐标；若不存在，请说明理由．

已知△ABC，延长BC到D，使CD=BC．取AB的中点F，连接FD交AC于点E．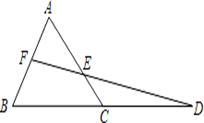

（1）求AE：AC的值；（2）若AB=a，FB=EC，求AC的长．

如图1，矩形ABCD的两条边在坐标轴上，点D与坐标原点O重合，且AD=8，AB=6．如图2，矩形ABCD沿OB方向以每秒1个单位长度的速度运动，同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动，当点P到达点C时，矩形ABCD和点P同时停止运动，设点P的运动时间为t秒．

（1）当t=5时，请直接写出点D、点P的坐标；
（2）当点P在线段AB或线段BC上运动时，求出△PBD的面积S关于t的函数关系式，并写出相应t的取值范围；
（3）点P在线段AB或线段BC上运动时，作PE⊥x轴，垂足为点E，当△PEO与△BCD相似时，求出相应的t值．

在矩形ABCD中，点P在AD上，AB=2，AP=1，将三角板的直角顶点放在点P处，三角板的两直角边分别能与AB、BC边相交于点E、F，连接EF．
（1）如图，当点E与点B重合时，点F恰好与点C重合，求此时PC的长；

（2）将三角板从（1）中的位置开始，绕点P顺时针旋转，当点E与点A重合时停止，在这个过程中，请你观察、探究并解答：

①∠PEF的大小是否发生变化？请说明理由；
②直接写出从开始到停止，线段EF的中点所经过的路线长．

（本题12分）如图，在平面直角坐标系中，矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上，OA=4，OC=2．点P从点O出发，沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D，点D随点P的运动而运动，连接DP、DA．

（1）请用含t的代数式表示出点D的坐标；
（2）求t为何值时，△DPA的面积最大，最大为多少？
（3）在点P从O向A运动的过程中，△DPA能否成为直角三角形？若能，求t的值．若不能，请说明理由；
（4）请直接写出随着点P的运动，点D运动路线的长．

以平面上一点O为直角顶点，分别画出两个直角三角形，记作△AOB和△COD，其中∠ABO=∠DCO=30．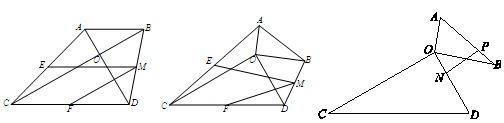

图1                         图2                     图3
（1）点E、F、M分别是AC、CD、DB的中点，连接FM、EM．
①如图1，当点D、C分别在AO、BO的延长线上时，=_______；
②如图2，将图1中的△AOB绕点O沿顺时针方向旋转角（），其他条件不变，判断的值是否发生变化，并对你的结论进行证明；
（2）如图3，若BO=，点N在线段OD上，且NO=2.点P是线段AB上的一个动点，在将△AOB绕点O旋转的过程中，线段PN长度的最小值为_______，最大值为_______．

（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）
已知：如图，是半圆的直径，弦，动点、分别在线段、上，且，的延长线与射线相交于点、与弦相交于点（点与点、不重合），，．设，的面积为．

（1）求证：；
（2）求关于的函数关系式，并写出它的定义域；
（3）当是直角三角形时，求线段的长．

如图，∠MON=90°，A、B分别是OM、ON上的点，OB=4．点C是线段AB的中点，将线段AC以点A为旋转中心，沿顺时针方向旋转90°，得到线段AD，过点B作ON的垂线．
（1）当点D恰好落在垂线上时，求OA的长；
（2）过点D作DE⊥OM于点E，将（1）问中的△AOB以每秒2个单位的速度沿射线OM方向平移，记平移中的△AOB为△，当点O′与点E重合时停止平移．设平移的时间为t秒，△与△DAE重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围；
（3）在（2）问的平移过程中，若与线段交于点P，连接，，，是否存在这样的t，使△是等腰三角形？若存在，求出t的值；若不存在，请说明理由．

木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：方案一：直接锯一个半径最大的圆；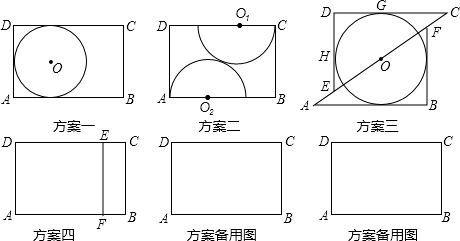

方案二：圆心O₁、O₂分别在CD、AB上，半径分别是O₁C、O₂A，锯两个外切的半圆拼成一个圆；
方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；
方案四：锯一块小矩形BCEF拼到矩形AFED下面，利用拼成的木板锯一个尽可能大的圆．
（1）写出方案一中圆的半径；
（2）通过计算说明方案二和方案三中，哪个圆的半径较大？
（3）在方案四中，设CE=x（0＜x＜1），圆的半径为y．
①求y关于x的函数解析式；
②当x取何值时圆的半径最大，最大半径为多少？并说明四种方案中哪一个圆形桌面的半径最大．