初中数学相似多边形的性质解答题

如图，在平面直角坐标系中，直角梯形OABC的边OC、OA分别与x轴、y轴重合，AB∥OC，∠AOC=90°，∠BCO=45°，BC=12，点C的坐标为（－18，0）。

（1）求点B的坐标；
（2）若直线DE交梯形对角线BO于点D，交y轴于点E，且OE=4，OD=2BD，求直线DE的解析式；
（3）若点P是（2）中直线DE上的一个动点，在坐标平面内是否存在点Q，使以O、E、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由。

如图，在平面直角坐标系中，已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上，并且OA、OB的长分别是方程x²—7x+12=0的两根(OA<0B)，动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．
(1)求A、B两点的坐标。
(2)求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．
(3)当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形?若存在，请直接写出M点的坐标；若不存在，请说明理由．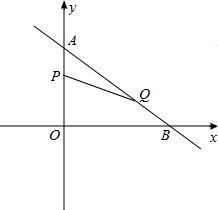

如图，在四边形ABCD中，对角线AC、BD相交于点E，且AC⊥BD，∠ADB=∠CAD+∠ABD，∠BAD=3∠CBD．
（1）求证：△ABC为等腰三角形；
（2）M是线段BD上一点，BM：AB=3：4，点F在BA的延长线上，连接FM，∠BFM的平分线FN交BD于点N，交AD于点G，点H为BF中点，连接MH，当GN=GD时，探究线段CD、FM、MH之间的数量关系，并证明你的结论．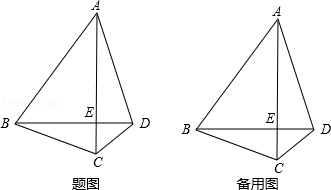

如图（1），E是正方形ABCD的边BC上的一个点（E与B、C两点不重合），过点E作射线EP⊥AE，在射线EP上截取线段EF，使得EF=AE；过点F作FG⊥BC交BC的延长线于点G．
（1）求证：FG=BE；
（2）连接CF，如图（2），求证：CF平分∠DCG；
（3）当时，求sin∠CFE的值．

如图1，在平面直角坐标系中，已知点A（－6，0），点B（0，8），点C在y轴上，将△OAB沿直线AC对折，使点O落在边AB上的点D处．

（1）求直线AB、AC的解析式．
（2）如图2，过B作BE⊥AC，垂足为E，若F为AB边上一动点，是否存在点F，使C为△EOF内心，若存在，请求出F点坐标，若不存在，请说明理由．

如图①，两个菱形ABCD和EFGH是以坐标原点O为位似中心的位似图形，对角线均在坐标轴上，已知菱形EFGH与菱形ABCD的相似比为1:2，∠BAD＝120°，其中AD＝4．
（1）点D坐标为     ，点E坐标为     ；
（2）固定图①中的菱形ABCD，将菱形EFCH绕O点顺时针方向旋转α度角（0°＜α＜90°），并延长OE交AD于P，延长OH交CD于Q，如图②所示，
①当α＝30°时，求点P的坐标；
②试探究：在旋转的过程中是否存在某一角度α，使得四边形AFEP是平行四边形？若存在，请推断出α的值；若不存在，说明理由；

已知抛物线经过A（1，0）、B（3，0）、C（0，3）三个点，

（1）求抛物线的解析式；
（2）如图（1），作△OBC的外接圆⊙Oˊ，D为BC上方半圆上一点，当tan∠COD=时，求OD的长；
（3）如图（2）直线y=x-2与抛物线交于E、F两点，与y轴交于点G，作y轴的平行线，分别与线段EF、抛物线交于P、Q两点（点P与E、F不重合），点K为射线PE上一点，当△PQK与△BAC相似时，求△PQK的最大面积。

已知，在矩形中，连接对角线，将绕点顺时针旋转得到，并将它沿直线向左平移，直线与交于点，连接，．
（1）如图①，当，点平移到线段上时，线段有怎样的数量关系和位置关系？直接写出你的猜想；
（2）如图②，当，点平移到线段的延长线上时，（1）中的结论是否成立，请说明理由；
（3）如图③，当时，对矩形进行如已知同样的变换操作，线段有怎样的数量关系和位置关系？直接写出你的猜想．

图①                        图②                图③

如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A，B，直线CD与x轴、y轴分别交于点C，D，AB与CD相交于点E，线段OA，OC的长是一元二次方程x²﹣18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=．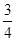
（1）求点A，C的坐标；
（2）若反比例函数y=的图象经过点E，求k的值；
（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．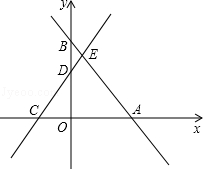

如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ACB＞∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E，试说明E是△ABC的自相似点．
（2）如图③，在△ABC中，∠A＜∠B＜∠C．
①利用尺规作出△ABC的自相似点P（不写出作法，保留作图痕迹）；
②如果△ABC的内心P是该三角形的自相似点，请直接写出该三角形三个内角的度数．

如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=6cm，BD=8cm，动点P，Q分别从点B，D同时出发，运动速度均为1cm/s，点P沿B→C→D运动，到点D停止，点Q沿D→O→B运动，到点O停止1s后继续运动，到B停止，连接AP，AQ，PQ．设△APQ的面积为y（cm²）（这里规定：线段是面积0的几何图形），点P的运动时间为x（s）．
（1）填空：AB=　  　cm，AB与CD之间的距离为　 　cm；
（2）当4≤x≤10时，求y与x之间的函数解析式；
（3）直接写出在整个运动过程中，使PQ与菱形ABCD一边平行的所有x的值．

已知梯形ABCD中，AD∥BC，AD=1，BC=2，sinB=，过点C在∠BCD的内部作射线交射线BA于点E，使得∠DCE=∠B．

（1）如图1，当ABCD为等腰梯形时，求AB的长；
（2）当点E与点A重合时（如图2），求AB的长；
（3）当△BCE为直角三角形时，求AB的长．

已知：正方形的边长为1，射线与射线交于点，射线与射线交于点，．

（1）如图1，当点在线段上时，试猜想线段、、有怎样的数量关系？并证明你的猜想．
（2）设，，当点在线段上运动时（不包括点、），如图1，求关于的函数解析式，并指出的取值范围．
（3）当点在射线上运动时（不含端点），点在射线上运动.试判断以为圆心以为半径的和以为圆心以为半径的之间的位置关系.

（4）当点在延长线上时，设与交于点，如图2．问△与△能否相似，若能相似，求出的值，若不可能相似，请说明理由．

如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．
（1）问题发现
①当时，；
②当时， 
（2）拓展探究
试判断：当0°≤α＜360°时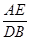，的大小有无变化？请仅就图2的情况给出证明．
（3）问题解决
当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长．

已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．

（1）如图，已知折痕与边BC交于点E，连结AP、EP、EA．求证：△ECP∽△PDA；
（2）若△ECP与△PDA的面积比为1：4，求边AB的长；
（3）在（2）的条件下以点A为坐标原点，AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系，问在坐标平面内是否存在点M，使得以点A、B、E、M为顶点的四边形是平行四边形，若存在请直接写出点M的坐标；若不存在请说明理由。