初中数学统计表试题

下表是随机抽取的某公司部分员工的月收入资料．

月收入/元	45000	18000	10000	5500	5000	3400	3000	2000
人数	1	1	1	3	6	1	11	2

（1）请计算以上样本的平均数和中位数；

（2）甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平，请你写出甲乙两人的推断结论；

（3）指出谁的推断比较科学合理，能真实地反映公司全体员工月收入水平，并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因．

为了帮助我市一名贫困学生，某校组织捐款，现从全校所有学生的捐款数额中随机抽取10名学生的捐款数统计如下表：

捐款金额/元	20	30	50	90
人数	2	4	3	1

则下列说法正确的是（　　）

A．	10名学生是总体的一个样本
B．	中位数是40
C．	众数是90
D．	方差是400

下表是博文学校初三•一班慧慧、聪聪两名学生入学以来10次数学检测成绩（单位：分）．

慧慧	116	124	130	126	121	127	126	122	125	123
聪聪	122	124	125	128	119	120	121	128	114	119

回答下列问题：

（1）分别求出慧慧和聪聪成绩的平均数；

（2）分别计算慧慧和聪聪两组数据的方差；

（3）根据（1）（2）你认为选谁参加全国数学竞赛更合适？并说明理由；

（4）由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱，学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动，求两名学生分别在初三•二班和初三•三班的概率．

近年来，我国持续的大面积的雾霾天气让环境和健康问题成为焦点，为了调查学生对雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了如图所示的不完整的三种统计图表．

对雾霾所了解程度的统计表：

对雾霾的了解程度	百分比
A．非常了解	5%
A．比较了解	15%
C．基本了解	45%
D．不了解	n

请结合统计图表，回答下列问题：

（1）本次参与调查的学生共有　　人，n＝　　；

（2）扇形统计图中D部分扇形所对应的圆心角是　　度；

（3）请补全条形统计图；

（4）根据调查结果，学校准备开展关于雾霾的知识竞赛，某班要从“非常了解”程度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去，否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．

自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：

使用次数	0	1	2	3	4	5（含5次以上）
累计车费	0	0.5	0.9			1.5

同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：

使用次数	0	1	2	3	4	5
人数	5	15	10	30	25	15

（Ⅰ）写出a，b的值；

（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利？说明理由．

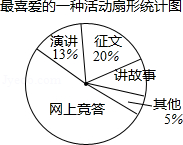
近期，我市中小学广泛开展了“传承中华文化，共筑精神家园”爱国主义读书教育活动，某中学为了解学生最喜爱的活动形式，以“我最喜爱的一种活动”为主题，进行随机抽样调查，收集数据整理后，绘制出以下两幅不完整的统计图表，请根据图中提供的信息，解答下面的问题：

最喜爱的一种活动统计表

活动形式	征文	讲故事	演讲	网上竞答	其他
人数	60	30	39

（1）在这次抽样调查中，一共调查了多少名学生？扇形统计图中“讲故事”部分的圆心角是多少度？

（2）如果这所中学共有学生3800名，那么请你估计最喜爱征文活动的学生人数．

甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：

甲	8	9	7	9	8	6	7	8	10	8
乙	6	7	9	7	9	10	8	7	7	10

且＝8，S_乙²＝1.8，根据上述信息完成下列问题：

（1）将甲运动员的折线统计图补充完整；

（2）乙运动员射击训练成绩的众数是　　，中位数是　　．

（3）求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．

为了深化课程改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校部分学生选择社团的意向．并将调查结果绘制成如下统计图表（不完整）：

选择意向	文学鉴赏	国际象棋	音乐舞蹈	书法	其他
所占百分比	a	20%	b	10%	5%

根据统计图表的信息，解答下列问题：

（1）求本次抽样调查的学生总人数及a、b的值；

（2）将条形统计图补充完整；

（3）若该校共有1300名学生，试估计全校选择“音乐舞蹈”社团的学生人数．

某校八年级学生在学习《数据的分析》后，进行了检测，现将该校八（1）班学生的成绩统计如下表，并绘制成条形统计图（不完整）．

分数（分）	人数（人）
68	4
78	7
80	3
88	5
90	10
96	6
100	5

（1）补全条形统计图；

（2）该班学生成绩的平均数为86.85分，写出该班学生成绩的中位数和众数；

（3）该校八年级共有学生500名，估计有多少学生的成绩在96分以上（含96分）？

（4）小明的成绩为88分，他的成绩如何，为什么？

为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则下列说法错误的是（　　）

阅读量（单位：本/周）	0	1	2	3	4
人数（单位：人）	1	4	6	2	2

A．中位数是2B．平均数是2C．众数是2D．极差是2

某校为了提升初中学生学习数学的兴趣，培养学生的创新精神，举办"玩转数学"比赛．现有甲、乙、丙三个小组进入决赛，评委从研究报告、小组展示、答辩三个方面为各小组打分，各项成绩均按百分制记录．甲、乙、丙三个小组各项得分如表：

小组	研究报告	小组展示	答辩
甲	91	80	78
乙	81	74	85
丙	79	83	90

（1）计算各小组的平均成绩，并从高分到低分确定小组的排名顺序；

（2）如果按照研究报告占40%，小组展示占30%，答辩占30%计算各小组的成绩，哪个小组的成绩最高？

某校足球队有16名队员，队员的年龄情况统计如下：

年龄 $/$ 岁	13	14	15	16
人数	3	5	6	2

则这16名队员年龄的中位数和众数分别是 $($ 　　 $)$

A．

14，15

B．

15，15

C．

14.5，14

D．

14.5，15

某公司有10名员工，他们所在部门及相应每人所创年利润如下表所示．

部门	人数	每人所创年利润 $/$ 万元
$A$	1	10
$B$	2	8
$C$	7	5

这个公司平均每人所创年利润是 　　万元．

我市某一周内每天的最高气温如下表所示：

最高气温 ${(}^{°}\text{C})$	25	26	27	28
天数	1	1	2	3

则这组数据的中位数和众数分别是 $($ 　　 $)$

A．

26.5和28

B．

27和28

C．

1.5和3

D．

2和3

空气质量按照空气质量指数大小分为六个级别，分别为：一级优、二级良、三级轻度污染、四级中度污染、五级重度污染、六级严重污染．级别越高，说明污染的情况越严重，对人体的健康危害也就越大．空气质量达到一级优或二级良的天气为达标天气，如图是长春市从2014年到2019年的空气质量级别天数的统计图表．

$2014-2019$ 年长春市空气质量级别天数统计表

空气质量级别 天数 年份	优	良	轻度污染	中度污染	重度污染	严重污染
2014	30	215	73	28	13	6
2015	43	193	87	19	15	8
2016	51	237	58	15	5	0
2017	65	211	62	16	9	2
2018	123	202	39	0	1	0
2019	126	180	38	16	5	0

根据上面的统计图表回答下列问题：

（1）长春市从2014年到2019年空气质量为"达标"的天数最多的是 　 　年．

（2）长春市从2014年到2019年空气质量为"重度污染"的天数的中位数为 　　天，平均数为 　　天．

（3）长春市从2015年到2019年，和前一年相比，空气质量为"优"的天数增加最多的是 　　年，这一年空气质量为"优"的天数的年增长率约为 　　（精确到 $1\%)$ ．

（空气质量为"优"的天数的增长率 $=\frac{\mathit{今年空气质量为}″优″\mathit{的天数}-\mathit{去年空气质量为}″优″\mathit{的天数}}{\mathit{去年空气质量为}″优″\mathit{的天数}}\times 100\%)$

（4）你认为长春市从2014年到2019年哪一年的空气质量好？请说明理由．