初中数学利用频率估计概率试题

下列说法中正确的是(▲)

A．“打开电视，正在播放《新闻联播》”是必然事件；

B．某次抽奖活动中奖的概率为，说明每买100张奖券，一定有一次中奖；

C．数据1，1，2，2，3的众数是3；

D．想了解台州市城镇居民人均年收入水平，宜采用抽样调查．

小球从A点入口往下落，在每个交叉口都有向左或向右两种可能，且可能性相等。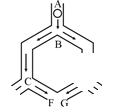

则小球最终从E点落出的概率为（   ）。

A．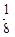

B．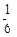

C．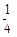

D．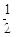

自连续正整数10~99中选出一个数，其中每个数被选出的机会相等。
求选出的数其十位数字与个位数字的和为9的机率为何？

A．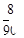

B．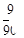

C．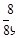

D．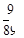

(本小题满分8分)

如图所示，有一个可以自由转动的圆形转盘，被平均分成四个扇形，四个扇形内分别标有数字1、2、－3、－4．若将转盘转动两次，每一次停止转动后，指针指向的扇形内的数字分别记为a、b（若指针恰好指在分界线上，则该次不计，重新转动一次，直至指针落在扇形内）．请你用列表法或树状图求a与 b的乘积等于2的概率．

小明的讲义夹放了大小相同的试卷共12页，其中语文4页、数学2页、英语6页，他随机地从讲义夹中抽出1页，抽出的试卷恰好是数学试卷的概率为（  ▲ ）

A．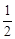

B．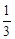

C．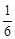

D．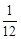

玉树地震灾区小朋友卓玛从某地捐赠的2种不同款式的书包和2种不同款式的文具盒中，分别取一个书包和一个文具盒进行款式搭配，则不同搭配的可能有　　　　种．

已知粉笔盒里只有2支黄色粉笔和3支红色粉笔，每支粉笔除颜色外均相同，现从中任取一支粉笔，则取出黄色粉笔的概率是（　　）

A．

B．

C．

D．

一家公司招考员工，每位考生要在A、B、C、D、E这5道试题中随机抽出2道题回答，规定答对其中1题即为合格．已知某位考生会答A、B两题，试求这位考生合格的概率．

有A，B两只不透明口袋，每只品袋里装有两只相同的球，A袋中的两只球上分别写了“细”、“致”的字样，B袋中的两只球上分别写了“信”、“心”的字样，从每只口袋里各摸出一只球，刚好能组成“细心”字样的概率是    （   ）

A．

B．

C．

D．

（本小题满分6分）“五·一”期间，某书城为了吸引读者，设立了一个可以自由转动的转盘（如图，转盘被平均分成12份），并规定：读者每购买100元的书，就可获得一次转动转盘的机会，如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么读者就可以分别获得45元、30元、25元的购书券，凭购书券可以在书城继续购书．

如果读者不愿意转转盘，那么可以直接获得10元的购书券．
（1）写出转动一次转盘获得45元购书券的概率；
（2）转转盘和直接获得购书券，你认为哪种方式对读者更合算？请说明理由．

一个口袋中装有10个红球和若干个黄球．在不允许将球倒出来数的前提下，为估计口袋中黄球的个数，小明采用了如下的方法：每次先从口袋中摸出10个球，求出其中红球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程20次，得到红球数与10的比值的平均数为0.4．根据上述数据，估计口袋中大约有       个黄球

在猜一商品价格的游戏中，参与者事先不知道该商品的价格，主持人要求他从图8的四张卡片中任意拿走一张，使剩下的卡片从左到右连成一个三位数，该数就是他猜的价格．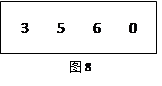

若商品的价格是360元，那么他一次就能猜中的概率是      ．

中央电视台举办的第14届“蓝色经典·天之蓝”杯青年歌手大奖赛，由部队文工团的A（海政）、B（空政）、C（武警）组成种子队，由部队文工团的D（解放军）和地方文工团的E（云南）、F（新疆）组成非种子队.现从种子队A、B、C与非种子队D、E、F中各抽取一个队进行首场比赛.
(1)请用适当方式写出首场比赛出场的两个队的所有可能情况（用代码A、B、C、D、E、F表示）；
(2)求首场比赛出场的两个队都是部队文工团的概率P.

下列说法正确的是（     ）．

A．买一张福利彩票一定中奖，是必然事件．

B．买一张福利彩票一定中奖，是不可能事件．

C．抛掷一个正方体骰子，点数为奇数的概率是．

D．一组数据：1，7，3，5，3的众数是3．