初中数学利用频率估计概率试题

某校为研究学生的课余爱好情况，采取抽样调查的方法，从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好，并将调查的结果绘制成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次研究中，一共调查了　　名学生；若该校共有1500名学生，估计全校爱好运动的学生共有　　名；

（2）补全条形统计图，并计算阅读部分圆心角是　　；

（3）在全校同学中随机选出一名学生参加演讲比赛，用频率估计概率，则选出的恰好是爱好阅读的学生概率是　　．

从甲地到乙地有，，三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：

公交车用时 公交车用时的频数 线路					合计
	59	151	166	124	500
	50	50	122	278	500
	45	265	167	23	500

早高峰期间，乘坐　　（填“”，“ ”或“” 线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．

如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．

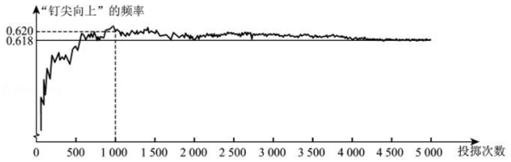
下面有三个推断：

①当投掷次数是500时，计算机记录"钉尖向上"的次数是308，所以"钉尖向上"的概率是0.616；

②随着试验次数的增加，"钉尖向上"的频率总在0.618附近摆动，显示出一定的稳定性，可以估计"钉尖向上"的概率是0.618；

③若再次用计算机模拟此实验，则当投掷次数为1000时，"钉尖向上"的频率一定是0.620．

其中合理的是 $($ 　　 $)$

A．

①

B．

②

C．

①②

D．

①③

林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：

移植的棵数 $n$	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数 $m$	865	1356	2220	3500	7056	13170	17580	26430
成活的频率 $\frac{m}{n}$	0.865	0.904	0.888	0.875	0.882	0.878	0.879	0.881

估计该种幼树在此条件下移植成活的概率为 　　．

在一个不透明的盒子中，共有“一白三黑”个围棋子，它们除了颜色之外没有其它区别．
（1）随机地从盒中提出子，则提出白子的概率是多少？
（2）随机地从盒中提出子，不放回再提第二子．请你用画树状图或列表的方法表示所有等可能的结果，并求恰好提出“一黑一白”子的概率．

在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	58	96	116	295	484	601
摸到白球的频率	0.58	0.64	0.58	0.59	0.605	0.601

 
（1）请估计：当n很大时，摸到白球的频率将会接近      ；（精确到0.1）
（2）试估算口袋中白种颜色的球有多少只？
（3）请画树状图或列表计算：从中先摸出一球，不放回，再摸出一球；这两只球颜色不同的概率是多少？

2015年国家实施“全面二孩政策”，人民医院迎来人口出生小高峰，某天出生了3个婴儿，假设生男生女的机会相同，那么这3个婴儿中，出现1个男婴、2个女婴的概率是多少？画出树状图或列表．

初三年级组织冬季拔河比赛，先用抽签的方法两两一组进行初赛，初三年级共有（1）（2）（3）（4）四个班，小明是初三（1）班的学生，他说“我们班和初三（2）班恰好分在同一组的概率是”你认为正确吗？如果正确，说明理由；如果不正确，写出正确的解答过程．

若100个产品中有95个正品、5个次品，从中随机抽取一个，恰好是次品的概率是        ．

九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动．在一个不透明的口袋中有三个完全相同的小球，把它们分别标号1、2、3．随机摸出一个小球记下标号后放回摇匀，再从中随机摸出一个小球记下标号．
（1）请用列表或画树形图的方法（只选其中一种），表示两次摸出小球上的标号的所有结果；
（2）规定当两次摸出的小球标号相同时中奖，求中奖的概率．

不透明的袋子中装有4个红球、3个黄球和5个蓝球，每个球除颜色不同外其它都相同，从中任意摸出一个球，则摸出        球的可能性最大．

有四张背面图案相同的卡片A、B、C、D，其正面分别画有四个不同的几何图形（如图）．小敏将这四张卡片背面朝上洗匀摸出一张，放回洗匀再摸出一张．

（1）用树状图（或列表法）表示两次摸出卡片所有可能的结果；（卡片可用A、B、C、D表示）
（2）求摸出的两张卡片图形都是中心对称图形的概率．

小颖为班级联欢会设计了一个“配紫色”游戏：下面是两个可以自由转动的转盘，每个转盘被分 成相等的几个扇形．游戏规则是：游戏者同时转动两个转盘，如果转盘 A 转出了红色，转盘 B 转出 了蓝色，那么配成了紫色．
（1）利用树状图或列表的方法计算配成紫色的概率．
（2）小红和小亮参加这个游戏，并约定配成紫色小红赢，两个转盘转出同种颜色，小亮赢．这个约定对双方公平吗？说明理由．

一个口袋中有 16 个白球和若干个黑球，在不允许将球倒出来的前提下，为估计口袋中黑球的
个数，采用了如下的方法：从口袋中摸出 1 个球记下颜色放回摇匀，不断重复上述过程多次，发现 摸到黑球的频率稳定在 0.8，根据上述数据，可估计口袋中大约有    个黑球．

甲、乙两名同学在一次用频率去估计概率的实验中，统一了某一结果出现的频率绘出的统计图 如图所示，则符合这一结果的实验可能是（  ）

A．从一个装有2个白球和1个红球的袋子中任取两球，取到两个白球的概率

B．任意写一个正整数，它能被 2 整除的概率

C．抛一枚硬币，连续两次出现正面的概率

D．掷一枚正六面体的骰子，出现 1 点的概率