有5张形状、大小和质地都相同的卡片,正面分别写有字母:A,B,C,D,E和一个等式,背面完全一致.现将5张卡片分成两堆,第一堆:A,B,C;第二堆:D,E,并从第一堆中抽出第一张卡片,再从第二堆中抽出第二张卡片.

(1)请用画树形图或列表法表示出所有可能结果;(卡片可用A,B,C,D,E表示)
(2)将“第一张卡片上x的值是第二张卡片中方程的解”记作事件M,求事件M的概率.
经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于5的概率.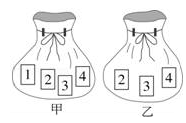
如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于5的概率.
小张、小王和另两名同学一起去看电影《寻龙诀》,小张买到4张座位相连的电影票,座位号顺次为8排3、4、5、6座.现在小张和小王从中随机各抽取一张电影票,求小张和小王抽取的电影票正好是相邻座位的概率(请通过画树状图或列表法写出分析过程).
九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口
袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随
机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为 .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,求满足关于x的方程x2+px+q=0有实数根的概率.
在不透明的布袋里装有白、红、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球有1个,红球有2个,黄球1个.
(1)求从袋中摸出一个球恰好是黄球的概率;
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是红球的概率.
一个不透明的口袋中有三个小球,上面分别标有数字1,2,3,每个小球,除数字外其他都相同.甲先从袋中随机取出1个小球,记下数字后放回;乙再从袋中随机取出1个小球记下数字.用画树状图或列表的方法,
(1)求取出的两个小球上的数字之和为3的概率;
(2)求取出的两个小球上的数字之和大于4的概率.
某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
在一个不透明的袋子中,分别装有写着整数3,4,5,6的四个质地、大小均相同的小球.
(1)从四个小球中任意抽取一个,则该小球上的数字是奇数的概率为P=______;
(2)从四个小球中随机地摸取一个小球不放回,再随机抽取一个小球,利用树状图或者列表法求两次球上的数字都小于6的概率.
小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,则他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
“一方有难,八方支援”.今年11月2日,鄂嘉出现洪涝灾害,牵动着全县人民的心,医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援鄂嘉防汛救灾工作.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中医生甲和护士A的概率.
试题篮
()