如图，是两个可以自由转动的转盘，甲转盘被等分成3个扇形，乙转盘被等分成4个扇形，每个扇形上都标有相应的数字。小亮和小颖利用它们做游戏，游戏规则是：同时转动两个转盘，当转盘停止后，指针所指区域内的数字之和小于10，小颖获胜；指针所指区域内的数字之和等于10，为平局；指针所指区域内的数字之和大于10，小亮获胜。如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止。
（1）请你用画树状图或列表的方法，求为平局的概率；
（2）你认为该游戏规则公平吗？为什么？如果不公平，
请你修改该游戏规则，使游戏公平。
某商场为了“五一”促销，举办抽奖活动，抽奖方案是：将如图的正六边形转盘等分成6个全等三角形，其中两个涂上灰色，顾客任意转动这个转盘2次，当转盘停止时，两次都指向灰色区域的即可获得奖品．
（1）求顾客获得奖品的概率；
（2）商场工作人员又提出了以下几个方案：
①抛掷一枚均匀的硬币3次，3次抛掷的结果都是正面朝上的即可获得奖品；
②一只不透明的袋子中，装有10个白球和20个红球，这些球除颜色外都相同，搅匀后从中任意摸出一个球，记下颜色后放回袋中并搅匀，再从中摸出一个球，两次都摸出白球的即可获得奖品；
③一只不透明的袋子中，装有2个白球和4个红球，这些球除颜色外都相同，搅匀后从中任意摸出两个球，两个都是白球的即可获得奖品；
④任意抛掷一枚均匀的骰子两次，两次朝上的点数都是3的倍数的即可获得奖品；
这几种方案中和原方案获奖概率相同的有 （填序号）．
甲、乙两个袋中均装有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标有的三个数值为﹣7，﹣1，3．乙袋中的三张卡片所标的数值为﹣2，1，6．先从甲袋中随机取出一张卡片，用x表示取出的卡片上的数值，再从乙袋中随机取出一张卡片，用y表示取出卡片上的数值，把x、y分别作为点A的横坐标和纵坐标．
（1）用适当的方法写出点A（x，y）的所有情况．
（2）求点A落在第一象限的概率．
甲、乙、丙三位同学用质地大小完全一样的纸片分别制作一张卡片a、b、c，收集后放在一个不透明的箱子中，然后每人从箱子中随机抽取一张．
（1）用列表或画树状图的方法表示三位同学抽到卡片的所有可能的结果；
（2）求三位同学中至少有一人抽到自己制作卡片的概率．
甲布袋中有三个红球，分别标有数字1，2，3；乙布袋中有三个白球，分别标有数字2，3，4．这些球除颜色和数字外完全相同．小亮从甲袋中随机摸出一个红球，小刚从乙袋中随机摸出一个白球．
（1）用画树状图（树形图）或列表的方法，求摸出的两个球上的数字之和为6的概率；
（2）小亮和小刚做游戏，规则是：若摸出的两个球上的数字之和为奇数，小亮胜；否则，小刚胜．你认为这个游戏公平吗？为什么？
把一副扑克牌中的3张黑桃牌（它们的正面牌面数字分别是3、4、5、）洗匀后正面朝下放在桌面上。
（1）如果从中抽取一张牌，那么牌面数字是4的概率是多少？
（2）小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽出一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽出一张牌，记下牌面数字。当2张牌面数字相同时，小王赢；当2张牌面数字不相同时，小李赢。现请你利用数状图或列表法分析游戏规则对双方是否公平？并说明理由。
不透明的口袋里装有红、黄、蓝三种颜色的小球若干个（除颜色外其余都相同），其中红球2个（分别标有1号、2号），蓝球1个．若从中任意摸出一个球，它是蓝球的概率为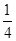
．
（1）求袋中黄球的个数；
（2）第一次任意摸出一个球（不放回），第二次再摸出一个球，请用画树状图或列表格的方法，求两次摸到不同颜色球的概率．
有四张背面相同的纸牌A、B、C、D，其正面分别画有四个不同的几何图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
（1）用画树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
（2）求摸出两张牌面图形都是中心对称图形的纸牌的概率．
小张和小罗玩一种转盘游戏，如图是两个完全相同的转盘，转盘一被分成面积相等的三个扇形，用数字“1”、“2”、“3”表示，转盘二被分成面积相等的四个扇形，用数字“1”、“2”、“3”、“4”表示，固定指针，同时转动两个转盘，任其自由停止，若两指针所指数字之积为偶数，则小张获胜；若两指针所指数字之积为奇数，则小罗获胜；若其中一个指针指向扇形的分界线，则都重转一次．你认为游戏是否公平？请说明理由．若不公平，请你修改游戏规则，使游戏公平．
有A、B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B 布袋中有三个完全相同的小球，分别标有数字−1，−2和−3．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为(x，y)．
（1）用列表或画树状图的方法写出点Q的所有可能坐标；
（2）求点Q落在直线y=-x−1上的概率．
在无锡市首届“文明风尚好少年”全媒体选拔大赛初赛中，甲、乙、丙三位评委对小选手的综合表现，分别给出“待定”（用字母W表示）或“通过”（用字母P表示）的结论．
（1）请用树状图表示出三位评委给小选手乐乐的所有可能的结论；
（2）对于小选手乐乐，只有甲、乙两位评委给出相同结论的概率是多少？
（3）比赛规定，三位评委中至少有两位给出“通过”的结论，则小选手可入围进入复赛，问乐乐进入复赛的概率是多少？
有A、B两个口袋，A口袋中装有两个分别标有数字2，3的小球；B口袋中装有三个分别标有数字
，4，
的小球．小明先从A口袋中随机取出一个小球，用m表示所取球上的数字，再从B口袋中随机取出两个小球，用n表示所取球上的数字之和．
（1）用树状图法或列表法表示小明所取出的三个小球的所有可能结果；
（2）求
的值是整数的概率．
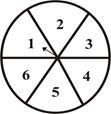
有时我们可以看到这样的转盘游戏：如图所示，你只要出1元钱就可以随意地转动转盘，转盘停止时指针落在哪个区域，你就按照这个区域所示的数字相应地顺时针跳过几格，然后按照下图所示的说明确定你的资金是多少.例如，当指针指向 “2”区域时候，你就向前跳过两个格到“5”，按奖金说明，“5”所示的资金为0.2元，你就可以得0.2元.请问这个游戏公平吗？能否用你所学的知识揭示其中的秘密？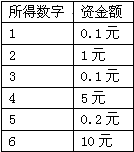
在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球，这三个小球除颜色外其他都相同，（1）在其中一个口袋中一次性随机摸出两个球，请写出在这一过程中的一个必然事件；
（2）若分别从两个袋中随机取出一个球，试求出两个小球颜色相同的概率。
试题篮
()
粤公网安备 44130202000953号
