(本题8分)小明去文具店购买2B铅笔,店主说:“如果多买一些,给你打8折”.小明测算了一下,如果买100支,比按原价购买可以便宜10元,求每支铅笔的原价是多少?
(本题10分) a、b都是正整数,设a b表示从a起b个连续正整数的和,例如:2
b表示从a起b个连续正整数的和,例如:2 3=2+3+4,5
3=2+3+4,5 4=5+6+7+8,已知x
4=5+6+7+8,已知x 5=2005,求x的值
5=2005,求x的值
“*”是规定的一种运算法则:a*b=a2-2b.
(1)求3*4的值为 ;
(2)若(-4)*x=8,求x的值;
(3)若2*(4*x)=2+x,求x的值.
规定一种新运算a⊙b=a2 -2b.
(1)求(-1)⊙2的值;
(2)若2⊙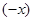 =6,求
=6,求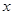 的值。
的值。
近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是12000元/ ,面积如图所示(单位:米,卫生间的宽未定,设宽为
,面积如图所示(单位:米,卫生间的宽未定,设宽为 米),售房部为张先生提供了以下两种优惠方案:
米),售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是12000元/ ,其中厨房可免费赠送
,其中厨房可免费赠送 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售.
(1)用 表示方案一中购买一套该户型商品房的总金额,用
表示方案一中购买一套该户型商品房的总金额,用 表示方案二中购买一套该户型商品房的总金额,分别求出两种方案中的总金额
表示方案二中购买一套该户型商品房的总金额,分别求出两种方案中的总金额 、
、 (用含x的式子表示);
(用含x的式子表示);
(2)求当x = 2时,两种方案的总金额分别是多少元?
(3)张先生因现金不够,在银行借了18万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率.
①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第 (
( ,
, 是正整数)个月的还款数额为P,请写出P与
是正整数)个月的还款数额为P,请写出P与 之间的关系式.
之间的关系式.
在“五一”黄金周期间,小明、小亮等同学随家人一同到江郎山游玩,看见门口有如下票价提示:“成人:35元/张;学生:按成人票5折优惠;团体票(16人以上含16人):按成人票价六折优惠”。
在购买门票时,小明与他爸爸有如下对话,爸爸:“大人门票每张35元,学生门票对折优惠,我们共有12人,共需350元”。小明:“爸爸,等一下,让我算一算,换一种方式买票是不是可以更省钱”。
问题:(1)小明他们一共去了几个成人,几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?说明理由
初一学生王马虎同学在做作业时,不慎将墨水瓶打翻,使一道作业只能看到:甲、乙两地相距160千米,摩托车的速度为45千米/时,运货汽车的速度为35千米/时,______________________________?请你将这道作业题补充完整并列出方程解答。
已知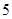 台
台 型机器一天的产品装满
型机器一天的产品装满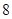 箱后还剩
箱后还剩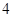 个,
个,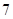 台
台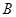 型机器一天的产品装满
型机器一天的产品装满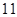 箱后还剩
箱后还剩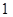 个,每台
个,每台 型机器比
型机器比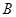 型机器一天多生产
型机器一天多生产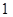 个产品,求每箱装有多少个产品?
个产品,求每箱装有多少个产品?
一件工作,甲单独做20小时完成,乙单独做12小时完成.现在先由甲单独做4小时,剩下的部分由甲、乙合做,需要几小时完成?
依据下列解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为 (____________)
(____________)
去分母,得3(3x+5)=2(2x﹣1).(____________)
去括号,得9x+15=4x﹣2.(____________)
(____________),得9x﹣4x=﹣15﹣2.(____________)
合并,得5x=﹣17.(____________)
(____________),得x= .(____________)
.(____________)
解下列方程
①
②解方程:
解:去分母,得 ……①
……①
即 ……②
……②
移项,得  ……③
……③
合并同类项,得  ……④
……④
∴ ……⑤
……⑤
上述解方程的过程中,是否有错误?答:__________;如果有错误,则错在__________步。如果上述解方程有错误,请你给出正确的解题过程:
③
④
(本题5分)列方程解应用题
甲、乙两站相距480千米,货车与客车同时从甲站出发开往乙站。已知客车的速度是货车的2.5倍,结果客车比货车早6小时到达乙站,求两种车的速度各是多少。
书正和子轩两人登一座山,书正每分钟登高10米,并且先出发30分钟,子轩每分钟登高15米,两人同时登上山顶.
(1)这座山有多高?
(2)如果将题中“书正先出发30分钟”这个条件改为“书正先爬山200米”其他条件不变,问子轩出发多少分钟追上书正?
试题篮
()