初中数学二元二次方程组解答题

(1)关于x的方程2x一3=2m+8的解是负数，求m的取值范围．
(2)如果代数式有意义，求x的取值范围．

（本题6分）先化简，再求值：，其中．

阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去，叫做分母有理化.
解决问题:
(1)的有理化因式是                 . 分母有理化得             .
(2)分母有理化:(1) ="_________;(2)" ="________;(3)" =______.．
(3)计算: .

先化简，再求值：，其中

观察下列等式：
①；
②；
③；
……
回答下列问题：
（1）仿照上列等式，写出第n个等式：                                     ;
（2）利用你观察到的规律，化简：；
（3）计算：

我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，
即已知三角形的三边长，求它的面积．用现代式子表示即为：
 ……①（其中、、为三角形的三边长，为面积）.
而另一个文明古国古希腊也有求三角形面积的海伦公式：
    ……②（其中）.
⑴ 若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积；
⑵ 你能否由公式①推导出公式②？请试试.

观察下列各式的化简过程
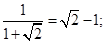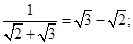①②③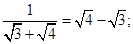
…;…
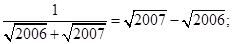（1）写出①式具体的化简过程。
（2）利用你所观察到的规律，试计算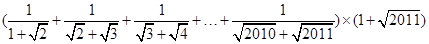
的值。

先化简，再求值：，其中a=+1，b=—1．

先化简，再求值.
(1) ,其中.
(2) 已知，求的值

一个正数的平方根是和，求这个正数．

请阅读下列材料：
问题：如图1，点，在直线的同侧，在直线上找一点，使得的值最小．小明的思路是：如图2，作点关于直线的对称点，连接，则与直线的交点即为所求．

请你参考小明同学的思路，探究并解决下列问题：
（1）如图3，在图2的基础上，设与直线的交点为，过点作，垂足为．若，，，写出的值为           ；
（2）将（1）中的条件“”去掉，换成“”，其它条件不变，写出此时的值            ；

（3）+的最小值为           ．       

先化简，再求值：，其中．

计算：
（1）          
（2）求（x-2）²=9中x的值．

请把下列各数填入相应的集合中．
-（-5），-4，0，-，，+1．666，-0．010010001…
正数集合：｛             …｝ 
分数集合：｛                 …｝
非负整数集合：｛         …｝ 
无理数集合：｛               …｝

求值（每小题4分，共8分）
（1）．             （2）；