某校5月份举行了八年级生物实验考查,有 和 两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验 考查的概率是 ;
(2)用列表或画树状图的方法求小明、小丽都参加实验 考查的概率;
(3)他们三人都参加实验 考查的概率是 .
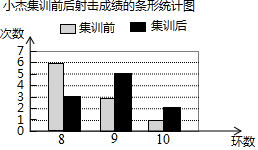
为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.
(1)集训前小杰射击成绩的众数为 ;
(2)分别计算小杰集训前后射击的平均成绩;
(3)请用一句话评价小杰这次集训的效果.
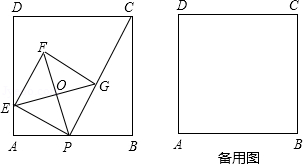
如图,已知正方形 的边长为4,点 是 边上的一个动点,连接 ,过点 作 的垂线交 于点 ,以 为边作正方形 ,顶点 在线段 上,对角线 、 相交于点 .
(1)若 ,则 ;
(2)①求证:点 一定在 的外接圆上;
②当点 从点 运动到点 时,点 也随之运动,求点 经过的路径长;
(3)在点 从点 到点 的运动过程中, 的外接圆的圆心也随之运动,求该圆心到 边的距离的最大值.
农经公司以30元 千克的价格收购一批农产品进行销售,为了得到日销售量 (千克)与销售价格 (元 千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格 (元 千克) |
30 |
35 |
40 |
45 |
50 |
日销售量 (千克) |
600 |
450 |
300 |
150 |
0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定 与 之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出 元 的相关费用,当 时,农经公司的日获利的最大值为2430元,求 的值.(日获利 日销售利润 日支出费用)
我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在 中, 是 边上的中线, 与 的“极化值”就等于 的值,可记为 △ .
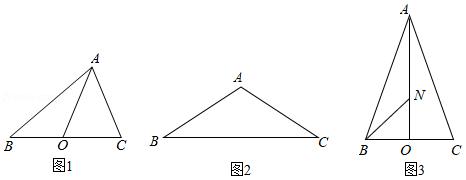
(1)在图1中,若 , , , 是 边上的中线,则 △ , △ ;
(2)如图2,在 中, , ,求 △ 、 △ 的值;
(3)如图3,在 中, , 是 边上的中线,点 在 上,且 .已知 △ , △ ,求 的面积.
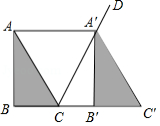
如图,将 沿着射线 方向平移至△ ,使点 落在 的外角平分线 上,连接 .
(1)判断四边形 的形状,并说明理由;
(2)在 中, , , ,求 的长.
星期天,小明和小芳从同一小区门口同时出发,沿同一路线去离该小区1800米的少年宫参加活动,为响应“节能环保,绿色出行”的号召,两人都步行,已知小明的速度是小芳的速度的1.2倍,结果小明比小芳早6分钟到达,求小芳的速度.
车辆经过润扬大桥收费站时,4个收费通道 、 、 、 中,可随机选择其中的一个通过.
(1)一辆车经过此收费站时,选择 通道通过的概率是 ;
(2)求两辆车经过此收费站时,选择不同通道通过的概率.
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 、 两点,与 轴的另一交点为点 .
(1)求抛物线的函数表达式;
(2)点 为直线 上方抛物线上一动点,
①连接 、 ,设直线 交线段 于点 , 的面积为 , 的面积为 ,求 的最大值;
②过点 作 ,垂足为点 ,连接 ,是否存在点 ,使得 中的某个角恰好等于 的2倍?若存在,求点 的横坐标;若不存在,请说明理由.

(探索发现)
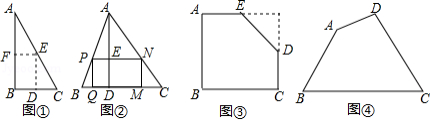
如图①,是一张直角三角形纸片, ,小明想从中剪出一个以 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线 、 剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
(拓展应用)
如图②,在 中, , 边上的高 ,矩形 的顶点 、 分别在边 、 上,顶点 、 在边 上,则矩形 面积的最大值为 .(用含 , 的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形” , , , , ,小明从中剪出了一个面积最大的矩形( 为所剪出矩形的内角),求该矩形的面积.
(实际应用)
如图④,现有一块四边形的木板余料 ,经测量 , , ,且 ,木匠徐师傅从这块余料中裁出了顶点 、 在边 上且面积最大的矩形 ,求该矩形的面积.
试题篮
()