如图,湿地景区岸边有三个观景台 、 、 .已知 米, 米, 点位于 点的南偏西 方向, 点位于 点的南偏东 方向.
(1)求 的面积;
(2)景区规划在线段 的中点 处修建一个湖心亭,并修建观景栈道 .试求 、 间的距离.(结果精确到0.1米)
(参考数据: , , , , , , .

某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元 斤,加工销售是130元 斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排 名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为 元,求 与 的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
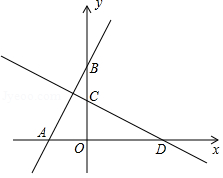
如图,在平面直角坐标系 中,过点 的直线交 轴正半轴于点 ,将直线 绕着点 顺时针旋转 后,分别与 轴、 轴交于点 、 .
(1)若 ,求直线 的函数关系式;
(2)连接 ,若 的面积是5,求点 的运动路径长.
某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为 分 .校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
“文明在我身边”摄影比赛成绩统计表
分数段 |
频数 |
频率 |
|
18 |
0.36 |
|
17 |
|
|
|
0.24 |
|
|
0.06 |
合计 |
|
1 |
根据以上信息解答下列问题:
(1)统计表中 的值为 ;样本成绩的中位数落在分数段 中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?

如图①,在平面直角坐标系中,二次函数 的图象与坐标轴交于 , , 三点,其中点 的坐标为 ,点 的坐标为 ,连接 , .动点 从点 出发,在线段 上以每秒1个单位长度的速度向点 作匀速运动;同时,动点 从点 出发,在线段 上以每秒1个单位长度的速度向点 作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为 秒.连接 .
(1)填空: , ;
(2)在点 , 运动过程中, 可能是直角三角形吗?请说明理由;
(3)在 轴下方,该二次函数的图象上是否存在点 ,使 是以点 为直角顶点的等腰直角三角形?若存在,请求出运动时间 ;若不存在,请说明理由;
(4)如图②,点 的坐标为 , ,线段 的中点为 ,连接 ,当点 关于直线 的对称点 恰好落在线段 上时,请直接写出点 的坐标.

(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中, 的三个顶点均在格点上.

(1)请按要求画图:将 绕点 按顺时针方向旋转 ,点 的对应点为 ,点 的对应点为 ,连接 ;
(2)在(1)所画图形中, .
(问题解决)
如图②,在等边三角形 中, ,点 在 内,且 , ,求 的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将 绕点 按顺时针方向旋转 ,得到△ ,连接 ,寻找 , , 三条线段之间的数量关系;
想法二:将 绕点 按逆时针方向旋转 ,得到△ ,连接 ,寻找 , , 三条线段之间的数量关系.
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
(灵活运用)
如图③,在四边形 中, ,垂足为 , , , , 为常数),求 的长(用含 的式子表示).
某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线 表示人均收费 (元)与参加旅游的人数 (人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?

, 两地被大山阻隔,若要从 地到 地,只能沿着如图所示的公路先从 地到 地,再由 地到 地.现计划开凿隧道 , 两地直线贯通,经测量得: , , ,求隧道开通后与隧道开通前相比,从 地到 地的路程将缩短多少?(结果精确到 ,参考数据: ,

如图,已知一次函数 的图象是直线 ,设直线 分别与 轴、 轴交于点 、 .
(1)求线段 的长度;
(2)设点 在射线 上,将点 绕点 按逆时针方向旋转 到点 ,以点 为圆心, 的长为半径作 .
①当 与 轴相切时,求点 的坐标;
②在①的条件下,设直线 与 轴交于点 ,与 的另一个交点为 ,连接 交 轴于点 ,直线 过点 分别与 轴、直线 交于点 、 ,当 与 相似时,求点 的坐标.

试题篮
()