已知关于x的一元二次方程x2 = 2（1－m）x－m2 的两实数根为x1，x2．
（1）求m的取值范围；
（2）设y = x1 + x2，当y取得最小值时，求相应m的值，并求出最小值．
今年春季，我国云南、贵州等西南地区遇到多少不遇旱灾，“一方有难，八方支援”，为及时灌溉农田，丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台（每种至少一台）及配套相同型号抽水机4台、3台、2台，每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时，灌溉农田32亩.
(1)设甲种柴油发电机数量为x台，乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量；
②求出y与x的函数关系式；
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元，应如何安排三种柴油发电机的数量，既能按要求抽水灌溉，同时柴油发电机总费用W最少？
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.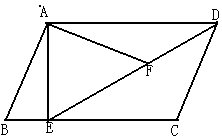
(1)求证：△ADF∽△DEC
(2)若AB＝4,AD＝3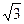
,AE＝3,求AF的长.
某市电话拨号上网有两种收费方式，用户可以任选其一：
(A)、计时制：3元每小时 ；
(B)、包月制：60元每月(限一部个人住宅电话上网)；此外，这一种上网方式得另加收通信费1.5元每小时。
某用户一个月内上网时间为多少小时两种收费方式支付的费用一样？
有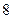
筐白菜，以每筐
千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的纪录如下：
回答下列问题：
（1）这筐白菜中最接近标准重量的这筐白菜重 千克；
（2）这筐白菜一共重多少千克？
如图，抛物线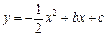
与x轴交于A、B两点（A点在B点左侧），与y轴交于点C，对称轴为直线
，OA = 2，OD平分∠BOC交抛物线于点D（点D在第一象限）．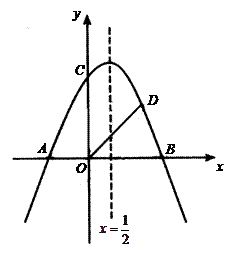
（１）求抛物线的解析式和点D的坐标；
（２）在抛物线的对称轴上，是否存在一点P，使得△BPD的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
（３）点M是抛物线上的动点，在x轴上是否存在点N，使A、D、M、N四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的M点坐标；如果不存在，请说明理由．
为了扶持农民发展农业生产，国家对购买农机的农户给予农机售价13%的政府补贴．某市农机公司筹集到资金130万元，用于一次性购进A、B两种型号的收割机共30台（购机费用不超过筹集资金）．根据市场需求，这些收割机可以全部销售，全部销售后利润不少于15万元．其中，收割机的进价和售价见下表：
| |
A型收割机 |
B型收割机 |
| 进价（万元/台） |
5.3 |
3.6 |
| 售价（万元/台） |
6 |
4 |
设公司计划购进A型收割机x台，收割机全部销售后公司获得的利润为y万元．
（１）试写出y与x的函数关系式；
（２）市农机公司有哪几种购进收割机的方案可供选择？
（３）选择哪种购进收割机的方案，农机公司获利最大？最大利润是多少？此种情况下，购买这30台收割机的所有农户获得的政府补贴总额W为多少万元？
在“传箴言”活动中，某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计，并制成了如下两幅不完整的统计图：
(1) 求该班团员在这一个月内所发箴言的平均条数是多少？并将该条形统计图补充完整；
(2) 如果发了3条箴言的同学中有两位男同学，发了4条箴言的同学中有三位女同学．现要从发了3条箴言和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会，请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．
已知：如图，在平面直角坐标系xOy中，直线
与
轴交于点A (– 2，0)，与反比例函数在第一象限内的图象交于点B (2，n)，连结BO，若
．
（1）求该反比例函数的解析式和直线的解析式；
（2）若直线AB与
轴的交点为C，求△OCB的面积．
试题篮
()
粤公网安备 44130202000953号
，其中
千米/时，3小时后两船相距多远？
，其中
．
测量，森林保护中心P在A城市的北偏东
和B城市的北偏西
的方向上，已知森林保护区的范围在以P点为圆心，50 km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：
）