图甲为“探究求合力的方法”的实验装置.
(1)下列说法中正确的是________.
| A.在测量同一组数据F1、F2和合力F的过程中,橡皮条结点O的位置不能变化 |
| B.弹簧测力计拉细线时,拉力方向必须竖直向下 |
| C.F1、F2和合力F的大小都不能超过弹簧测力计的量程 |
| D.为减小测量误差,F1、F2方向间夹角应为90° |
(2)弹簧测力计的指针如图乙所示,由图可知拉力的大小为________N.
如图甲所示,在圆柱体上放一物块P,圆柱体绕水平轴O缓慢转动,从A转至A′的过程,物块与圆柱体保持相对静止,则图乙反映的是该过程中( )

| A.重力随时间变化的规律 | B.支持力随时间变化的规律 |
| C.摩擦力随时间变化的规律 | D.合外力随时间变化的规律 |
如图所示,一光滑半圆形碗固定在水平面上,质量为m1的小球用轻绳跨过碗口并连接质量分别为m2和m3的物体,平衡时碗内小球恰好与碗之间没有弹力,两绳与水平方向夹角分别为53°、37°,则m1:m2:m3的比值为(已知sin53°=0.8,cos53°=0.6)( )

| A.5:4:3 | B.4:3:5 | C.3:4:5 | D.5:3:4 |
如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )

| A.f1=μ1 Mg f2=μ1 mg |
| B.f1=μ1(M+m)g f2=μ1 mg |
| C.f1=μ1Mg f2=μ2mg |
| D.f1=μ1(M+m)g f2=μ2 mg |
如图所示,物体的质量为2kg,两根轻细绳AB和AC一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平成θ=60°的拉力,若要使绳都能伸直,求拉力F的大小范围?(取g=10 m/s2)
右图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜面AB=10 cm,直角边AC=2 cm.当用F=100 N的力沿水平方向推劈时,求劈的上侧面和下侧面产生的推力.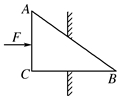
如图,一小球放置在木板与竖直墙面之间。设墙面对球的压力大小为N1,球对木板的压力大小为N2。以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置。不计摩擦,在此过程中 ( )

| A.N1始终减小,N2始终增大 |
| B.N1始终减小,N2始终减小 |
| C.N1先增大后减小,N2始终减小 |
| D.N1先增大后减小,N2先减小后增大 |
如图所示,用一根长为L的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹30°角且绷紧,小球A处于静止,则需对小球施加的最小力等于( )

A.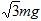 |
B. |
C.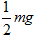 |
D. |
如图甲所示,质量均匀分布的A.B两球完全相同,质量均为m,用两根等长的细线悬挂在O点,两球之间固连着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为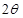 ,已知下列各情况中,弹簧与AB两球新连线始终共线,求:
,已知下列各情况中,弹簧与AB两球新连线始终共线,求: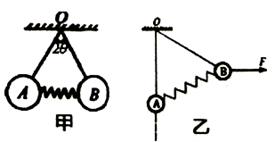
(1)AB两球均静止时,弹簧的长度被压缩了多少。
(2)现对B施加一水平向右大小为F的恒力,使得OA线竖直绷紧,如图乙,求AB两球均静止时弹簧的形变量。
(3)求上述(2)中OB线中张力的大小。
如图,将一质量为m的物块放置与倾角为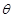 的粗糙斜面上,用一水平向右推力F作用于物块上,刚好能使物块匀速上滑,设物块与斜面间的动摩擦因数为μ,重力加速度为g,作出物块的受力示意图并求F的大小。
的粗糙斜面上,用一水平向右推力F作用于物块上,刚好能使物块匀速上滑,设物块与斜面间的动摩擦因数为μ,重力加速度为g,作出物块的受力示意图并求F的大小。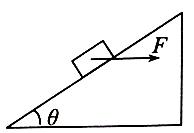
在“探究求合力的方法”实验中现有木板、白纸、图钉、橡皮筋、细绳套和一把弹簧秤
(1)为完成实验,某同学另找来一根弹簧,先测量其劲度系数,得到的实验数据如下表
根据表中数据在图甲中作出F-x图像并求得改弹簧的劲度系数k=_________N/m
(2)某次实验中,弹簧秤的指针位置如上图乙所示,其读数为_____N;同时利用(1)中结果获得弹簧上的弹力值为2.50N。请在答题卡虚线框中画出这两个共点力的合力 的图示;
的图示;
(3)由图得到 =________N。
=________N。
已知两个共点力的合力为F,如果它们之间的夹角固定不变,使其中的一个力增大,则
| A.合力F一定增大 | B.合力F的大小可能不变 |
| C.合力F可能增大 | D.合力F可能减小 |
粗糙长木板l的一端固定在铰链上,小物体放在木板上,开始时木板静止于水平位置,如图所示。使木板沿顺时针方向转动,在θ角逐渐增大的过程中,小物体所受木板摩擦力Ff的大小随θ角变化的关系是
如图所示,A, B为两个质量均为m,半径材质都相同的篮球,充足气后在两竖直放置的平行板之间由静止释放,两者一起以加速度a=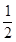 g做匀加速直线运动,已知运动过程中两球之间的弹力F=
g做匀加速直线运动,已知运动过程中两球之间的弹力F=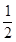 mg,忽略两球之间的摩擦,两球心连线与水平方向成30°角,忽略空气阻力,则平行板对A球的作用力大小为
mg,忽略两球之间的摩擦,两球心连线与水平方向成30°角,忽略空气阻力,则平行板对A球的作用力大小为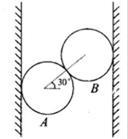
A.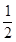 mg mg |
B.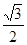 mg mg |
C.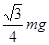 |
D.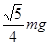 |
试题篮
()