(1)要使物体沿水平方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
(2)要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?已知取无穷远处引力势能为零时,物体距星球球心距离r时的引力势能为: . (G为万有引力常量)
. (G为万有引力常量)
地球质量为M,半径为R,万有引力恒量为G。若已知第一宇宙速度 =7.9k/s,地球半径R=6.4×103km,万有引力恒量G=6.67×10
=7.9k/s,地球半径R=6.4×103km,万有引力恒量G=6.67×10 N·m2·kg
N·m2·kg 。
。
求:(1)第一宇宙速度的计算式;
(2)地球的质量(要求保留两位有效数字)。
“神舟十号”飞船发射后,先进入一个椭圆轨道,经过多次变轨进入距地面高度为h的圆形轨道.已知飞船质量为m,地球半径为R,地球表面的重力加速度为g.设飞船进入圆形轨道后运动时的动能为EK,则( )
A.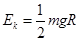 |
B.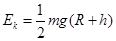 |
C.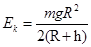 |
D.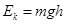 |
)2007年11月5日,嫦娥一号探月卫星进入绕月轨道开始进行对月球的科学探测.已知月球的半径约为地球半径的1/4,月球的质量约为地球质量的1/96.(地球表面的量力加速度g取10 m/s2,第一宇宙速度为7.9 km/s, )
)
(1)月球表面的重力加速度大约是多少?
(2)在月球上要发射一颗环月卫星,则最小发射速度大约为多少?
(3)若飞船登月成功时,宇航员借助一计时表测出近月飞船绕月球一周所需的时间为丁,请你写出月球平均密度的表达式.
一组宇航员乘坐太空穿梭机S,去修理位于离地球表面 的圆形轨道上的太空望远镜H。机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜则在穿梭机前方数千米处,如图所示。已知地球半径为
的圆形轨道上的太空望远镜H。机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜则在穿梭机前方数千米处,如图所示。已知地球半径为 ,地球表面重力加速度为
,地球表面重力加速度为 ,第一宇宙速度为
,第一宇宙速度为 。
。
(1)穿梭机所在轨道上的重力加速度 为多少?在穿梭 机内,一质量为m=70kg的宇航员受的重力
为多少?在穿梭 机内,一质量为m=70kg的宇航员受的重力 是多少?
是多少?
(2)计算穿梭机在轨道上的速率 。
。
(3)穿梭机需先进入半径较小的轨道,才有较大的角速度追上望远镜,试判断穿梭机要进入较低轨道时应增加还是减小其原有速率,试说明理由。
已知地球的半径R≈6.4×106m,地球表面的重力加速度g≈10m/s2,万有引力恒量G≈6.7×10-11N·kg2/m2。由此推导并估算:(把结果只保留一位有效数字即可)
(1)地球的质量M约为多少?
(2)近地环绕卫星的最大线速度v1约为多少?
宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用,设每个星体的质量均为m,四颗星稳定地分布在边长为a的正方形的四个顶点上,已知这四颗星均围绕正方形对角线的交点做匀速圆周运动,引力常量为G,试求:
(1)求星体做匀速圆周运动的轨道半径;
(2)若实验观测得到星体的半径为R,求星体表面的重力加速度;
(3)求星体做匀速圆周运动的周期.
宇航员在一行星上以10m/s的初速度竖直上抛一质量为0.2kg的物体,不计阻力,经2.5s后落回手中,已知该星球半径为7220km。
(1)该星球表面的重力加速度 多大?
多大?
(2)要使物体沿水平方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
(3)若物体距离星球无穷远处时其引力势能为零,则当物体距离星球球心r时其引力势能 (式中m为物体的质量,M为星球的质量,G为万有引力常量)。问要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
(式中m为物体的质量,M为星球的质量,G为万有引力常量)。问要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大?
已知太阳光从太阳射到地球,需要8分20秒,地球公转轨道可近似看成固定圆轨道,地球半径约为6.4×106 m, 试估算太阳质量M与地球质量m之比M/m为多少?(保留一位有效数字)
宇航员在一行星上以速度v0竖直上抛一质量为m的物体,不计空气阻力,经t秒后落回手中,已知该星球半径为R.若在该星球上离表面高h处以速度v0平抛一物体, 落地点离抛出点的距离多大?
某行星昼夜转动时间T0=8h,若用一弹簧测力计去测量同一物体的重力,结果在行星赤道上比它在两极处小9﹪.设想该行星自转角速度加快,在赤道上的物体将完全失重.则此行星自转周期多大?(行星看作标准球体)
试题篮
()