两条光滑的水平金属导轨彼此平行,置于桌边,金属棒ab架在两导轨端点上并与导轨垂直,导轨区域内有竖直向下的匀强磁场,导轨另一端与电池、电容器连成电路,如图15-2-11所示.已知金属棒的质量m=5×10-3kg,两导轨间距L="1.0" m,电池电动势E="16" V,电容器的电容量C="200" μF,磁场的磁感应强度B="0.5" T,金属棒在通电后受安培力作用而平抛出去,下落高度h="0.8" m,抛出落地水平位移S="0.064" m.试求开关K先接1,再接2,金属棒被抛出后电容器上电压的数值.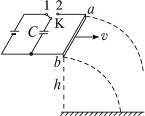
图15-2-11
如图所示,两根平行光滑金属导轨ab和cd置于同一水平面上,相互间隔为L="0.1" m,质量m="3" g的金属棒置于轨道右端,跨在两根导轨上,导轨左端通过开关S与电池连接,匀强磁场方向垂直轨道所在平面向上,磁感应强度B="0.1" T,轨道平面距地面高度h="0.8" m.接通开关S时,金属棒由于受安培力作用被水平抛出,落地点水平距离s′="2" m.取g="10" m/s2,求接通S瞬间,金属棒中通过的电荷量是多大?(假设接通S瞬间,金属棒中通过的是恒定电流)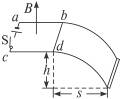
如图所示,两根平行放置的导电轨道,间距为L,倾角为θ,轨道间接有电动势为E(内阻不计)的电源.现有一根质量为m、电阻为R的金属杆ab垂直放于导电轨道上静止.轨道的摩擦和电阻均不计.要使ab杆静止,磁感应强度应为____________.
如图所示,一根均匀的导体棒ab,长为l,质量为m,电阻为R0,处在磁感应强度为B的匀强磁场中,导体ab由两根相同的轻质弹簧悬挂,并处在水平位置,这时每根弹簧的伸长量为x0.若电源电动势为E,电阻不计,两根弹簧的总电阻为R,求当开关S闭合后,导体ab平衡时每根弹簧的伸长量x是多少?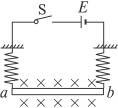
将一根长为L的直导线,由中点折成直角形放在磁感应强度为B的匀强磁场中,导线所在平面与磁感线垂直.当导线中通以电流I后,磁场对导线作用力大小为( )
| A.IBL | B. |
C. |
D. |
如图所示,接通开关S的瞬间,用丝线悬挂于一点可自由转动的通电直导线AB将( )
| A.A端向上,B端向下,悬线张力不变 |
| B.A端向下,B端向上,悬线张力不变 |
| C.A端向纸外,B端向纸内,悬线张力变小 |
| D.A端向纸内,B端向纸外,悬线张力变大 |
如图15-2-16所示,水平放置的光滑金属导轨M、N,平行地置于匀强磁场中,间距为d,磁场的磁感应强度大小为B,方向与导轨平面夹角为α.金属棒ab的质量为m,放在导轨上且与导轨垂直,电源电动势为E,定值电阻为R,其余部分电阻不计.则当电键K合上时,棒ab受到的安培力的大小为_____________,方向为_____________,棒的加速度大小为_____________.
图15-2-16
以下说法中正确的是( )
| A.通电导线在某处所受安培力为零,那么该处的磁感应强度必定为零 |
B.若长为L,电流为I的导线在某处受到的安培力为F,则该处的磁感强度必为 |
| C.如果将一段短导线(有电流)放入某处,测得该处的磁感强度为B,若撤去该导线,该处的磁感强度为零 |
| D.以上说法均不正确 |
如图所示,在磁感应强度B="1.0" T、方向竖直向下的匀强磁场中,有一个与水平面成θ=37°角的导电滑轨,滑轨上放一个可以自由滑动的金属杆ab,已知接在滑轨中的电源电动势E="12" V,内阻不计,ab杆长L="0.5" m,质量m="0.2" kg,杆与平行滑轨间的动摩擦因数μ=0.1;不计滑轨与ab杆的电阻,取g="10" m/s2,sin37°=0.6.求接在滑轨上的变阻器R的阻值在什么范围内变化时,可以使ab杆在滑轨上保持静止?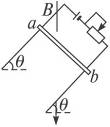
把长L=0.15m的导体棒置于磁感应强度B=1.0×10-2 T的匀强磁场中,使导体棒和磁场方向垂直,如图所示.若导体棒中的电流I="2.0" A,方向向左,则导体棒受到的安培力大小F=___________N,安培力的方向为竖直向___________.(选填“上”或“下”)
如图9所示,有一磁感应强度B=9.1×10-4T的匀强磁场,C、D为垂直于磁场的同一平面内的两点,它们之间的距离l=0.05m,今有一电子在此磁场中运动,它经过C点时的速度v的方向和磁场方向垂直,且与CD间的夹角α=30°,问:
(1)电子在C点时所受的洛仑兹力的方向如何?
(2)若此电子在运动中后来又经过了D点,则它的速度v应是多大?
(3)电子从C点到D点所用的时间是多少(电子的质量m=9.1×10-31kg,电子的电量e=1.6×10-19C)?
根据科普资料介绍,受控核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的”容器”可装,而是借助磁场能约束带电粒子运动这一理论,从而使高速运动的带电粒子束缚在某一磁场区域内,那么,该磁场就成了某种意义上的容器了。
(1)实践表明,如果氦核在磁场区域内沿垂直于磁场方向运动,速度大小V与它在磁场中运动的轨道半径R有关,根据我们已学过的知识,试推导出V与R的关系式。(已知氦核的荷质比为q/m,磁场的磁感强度为B,氦核重力不计)
(2)对于上面的”容器”,我们现按下面的简化条件来讨论:如图所示是一个截面为内径R1,外径R2的环状区域,区域内有垂直于截面的匀强磁场,已知氦核的荷质比为q/m,磁场的磁感强度为B,若氦核平行于截面从A点以相同速率沿各个方向射入磁场都不能穿出磁场外边界,求氦核的最大速度。
试题篮
()