阿尔法磁谱仪用于探测宇宙中的反物质和暗物质(即由“反粒子”构成的物质),如氚核( )的反粒子为(
)的反粒子为(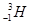 )。该磁谱仪核心部分截面区域是半径为r的圆形磁场,磁场方向垂直纸面向外,如图所示,P为入射窗口,各粒子从P射入速度相同,均沿直径方向,Pabcde为圆周上等分点,如反质子射入后打在e点,则氚核粒子射入将打在( )
)。该磁谱仪核心部分截面区域是半径为r的圆形磁场,磁场方向垂直纸面向外,如图所示,P为入射窗口,各粒子从P射入速度相同,均沿直径方向,Pabcde为圆周上等分点,如反质子射入后打在e点,则氚核粒子射入将打在( )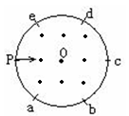
| A.a | B.b | C.d | D.c |
(12分)在如图所示的直角坐标系xoy中,矩形区域oabc内有垂直于纸面向外的匀强磁场,磁感应强度大小为B=5.0×10-2T;第一象限内有沿-y方向的匀强电场,电场强度大小为E=1.0×105N/C.已知矩形区域oa边长为0.60m,ab边长为0.20 m.在bc边中点N处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为 m/s的某种带正电粒子,带电粒子质量m=1.6×10-27kg,电荷量为q=+3.2×10-19kg,不计粒子重力,求:(计算结果保留两位有效数字)
m/s的某种带正电粒子,带电粒子质量m=1.6×10-27kg,电荷量为q=+3.2×10-19kg,不计粒子重力,求:(计算结果保留两位有效数字)
(1)粒子在磁场中运动的半径;
(2)从x轴上射出的粒子中,在磁场中运动的最短路程为多少?
(3)放射源沿-x方向射出的粒子,从射出到从y轴离开所用的时间.
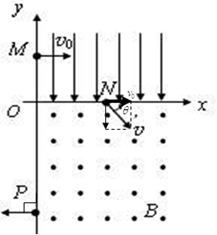
三个质子1、2和3分别以大小相等、方向如图所示的初速度v1、v2和v3经过平板MN上的小孔O射入匀强磁场B,磁场方向垂直纸面向里,整个装置处在真空中,且不计重力。最终这三个质子打到平板MN上的位置到小孔的距离分别为s1、s2和s3,则
| A.s1<s2<s3 | B.s2>s3>s1 | C.s1=s3>s2 | D.s1=s3<s2 |
1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖。若一束粒子由左端射入质谱仪后的运动轨迹如图所示,则下列说法中正确的是( )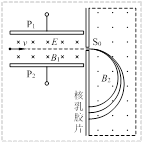
| A.该束带电粒子带负电 |
| B.速度选择器的P1极板带正电 |
| C.在B2磁场中运动半径越大的粒子,质量越大 |
| D.在B2磁场中运动半径越大的粒子,荷质比越小 |
如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中:
| A.运动时间相同 |
| B.运动轨道半径相同 |
| C.重新回到x轴时速度大小和方向均相同 |
| D.重新回到x轴时距O点的距离相同 |
如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度 从
从 点沿直径
点沿直径 方向射入磁场,经过
方向射入磁场,经过 时间从
时间从 点射出磁场,
点射出磁场, 与
与 成60°角。现将带电粒子的速度变为
成60°角。现将带电粒子的速度变为 /3,仍从
/3,仍从 点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为 ( )
点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为 ( )
A.  |
B.2 |
C.  |
D.3 |
如图所示装置中,区域Ⅰ中有竖直向上的匀强电场,电场强度为E,区域Ⅱ内有垂直纸面向外的水平匀强磁场,磁感应强度为B。区域Ⅲ中有垂直纸面向里的水平匀强磁场,磁感应强度为2B。一质量为m、带电量为q的带负电粒子(不计重力)从左边界O点正上方的M点以速度v0水平射入电场,经水平分界线OP上的A点与OP成60°角射入Ⅱ区域的磁场,并垂直竖直边界CD进入Ⅲ区域的匀强磁场中。求:
(1)粒子在Ⅱ区域匀强磁场中运动的轨道半径
(2)O、M间的距离
(3)粒子从M点出发到第二次通过CD边界所经历的时间
如图所示,在半径为R的圆内,有一磁感应强度为B的向外的匀强磁场,一质量为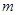 ,电量为
,电量为 的粒子(不计重力),从A点对着圆心方向垂直射入磁场,从C点飞出,则
的粒子(不计重力),从A点对着圆心方向垂直射入磁场,从C点飞出,则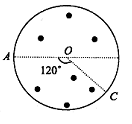
| A.粒子的轨道半径为R |
B.粒子的轨道半径为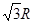 |
C.粒子在磁场中运动的时间为 |
D.粒子在磁场中运动的时间为 |
如图所示,在平面直角坐标系xOy中,第I象限存在沿y轴负方向的匀强电场,第IV象限存在垂直于坐标平面向外的匀强磁场,一带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经偏转电场后到达x轴上的N点,然后射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,已知M点的坐标是(0,h),N点的坐标是(2h,0),不计粒子重力,求: 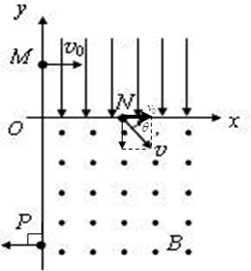
(1)粒子到达N点时的速度v的大小以及v与初速度v0的夹角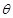 ;
;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从M点运动到P点的总时间t。
如图所示,在边长为L的正方形的区域abcd内,存在着垂直纸面向里的匀强磁场。今有一质量为m、电荷量为q的带正电粒子,以速度v从ad的中点e,垂直于磁场方向射入磁场,不计带电粒子的重力,要使该粒子恰从b点射出磁场

(1)带电粒子在磁场中运动的半径
(2)磁感应强度的大小。
如图所示.带正电粒子的质量为m,以速度v沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场中,磁场的磁感应强度为B,磁场的宽度为 ,若带电粒子离开磁场时的速度偏转角
,若带电粒子离开磁场时的速度偏转角 ,不计带电粒子的重力
,不计带电粒子的重力
(1)求带电粒子的电荷量
(2)求带电粒子在磁场中运动的时间
如图所示,两导体板水平放置,两板间电势差为U,带电粒子(不计重力)以某一初速度v0沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁场方向射入边界线竖直的匀强磁场,则粒子射入磁场和射出磁场的M、N两点间的距离d随着U和v0的变化情况为
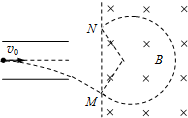
| A.d随v0增大而增大,d与U无关 |
| B.d随v0增大而增大,d随U增大而增大 |
| C.d随U增大而增大,d与v0无关 |
| D.d随v0增大而增大,d随U增大而减小 |
质量和电量都相等的带电粒子M和N(不计重力),以不同的速度率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图两种虚线所示,下列表述正确的是
| A.M带负电,N带正电 |
| B.M的速度率小于N的速率 |
| C.洛伦磁力对M、N做正功 |
| D.M的运行时间大于N的运行时间 |
如图所示,两平行金属板E、F之间电压为U,两足够长的平行边界MN、PQ区域内,有垂直纸面向外的匀强磁场,磁感应强度为B。一质量为m、带电量为+q的粒子(不计重力),由E板中央处静止释放,经F板上的小孔射出后,垂直进入磁场,且进入磁场时与边界MN成60°角,最终粒子从边界MN离开磁场。求:
(1)粒子在磁场中做圆周运动的半径r;
(2)两边界MN、PQ的最小距离d;
(3)粒子在磁场中运动的时间t。
(13分) 如图,边长L="0.2" m的正方形abcd区域(含边界)内,存在着垂直于区域的横截面(纸面)向外的匀强磁场,磁感应强度B=5.0×10-2T。带电平行金属板MN、PQ间形成了匀强电场E(不考虑金属板在其它区域形成的电场),MN放在ad边上,两板左端M、P恰在ab边上,两板右端N、Q间有一绝缘挡板EF。EF中间有一小孔O,金属板长度、板间距、挡板长度均为l="0.l" m。在M和P的中间位置有一离子源S,能够正对孔O不断发射出各种速率的带正电离子,离子的电荷量均为q=3.2×l0-19 C,质量均为m=6.4×l0-26 kg。不计离子的重力,忽略离子之间的相互作用及离子打到金属板或挡板上后的反弹。
(l)当电场强度E=104N/C时,求能够沿SO连线穿过孔O的离子的速率。
(2)电场强度取值在一定范围时,可使沿SO连线穿过O并进入磁场区域的离子直接从
bc边射出,求满足条件的电场强度的范围。
试题篮
()