设 、
、 为两条不同的直线,
为两条不同的直线, 、
、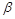 为两个不同的平面,给出下列命题:
为两个不同的平面,给出下列命题:
① 若 ∥
∥ ,
, ∥
∥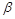 ,则
,则 ∥
∥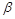 ;
;
② 若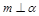 ,
,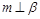 ,则
,则 ∥
∥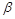 ;
;
③ 若 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;
;
④ 若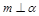 ,
,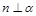 ,则
,则 ∥
∥ ;
;
上述命题中,所有真命题的序号是 ( )
| A.①② | B.③④ | C.①③ | D.②④ |
【选修4-5:不等式选讲】
设函数f(x)=|2x﹣1|﹣|x+2|.
(Ⅰ)解不等式f(x)>0;
(Ⅱ)若∃x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.
【选修4-4:坐标系与参数方程】
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA|•|PB|=1,求实数m的值.
【选修4-1:几何证明选讲】
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边上的中点,连接OD交圆O与点M.
(1)求证:DE是圆O的切线;
(2)求证:DE•BC=DM•AC+DM•AB.
如图,多面体ABCDEF中,底面ABCD是菱形,∠BCD=60°,四边形BDEF是正方形且DE⊥平面ABCD.
(Ⅰ)求证:CF∥平面ADE;
(Ⅱ)若 ,求多面体ABCDEF的体积V.
,求多面体ABCDEF的体积V.
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.1月某日某省x个监测点数据统计如下:

(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
试题篮
()