对变量x,y观测数据(x1,y1)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u1,v1)(i=1,2,…,10),得散点图2.由这两个散点图可以判断.( )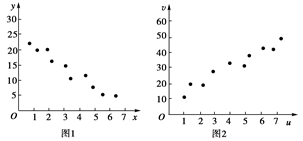
| A.变量x与y正相关,u与v正相关 |
| B.变量x与y正相关,u与v负相关 |
| C.变量x与y负相关,u与v正相关 |
| D.变量x与y负相关,u与v负相关 |
某校为了解高二学生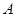 、
、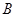 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试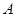 、
、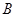 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2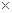 2列联表:
2列联表:
| |
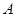 学科合格人数 学科合格人数 |
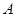 学科不合格人数 学科不合格人数 |
合计 |
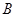 学科合格人数 学科合格人数 |
40 |
20 |
60 |
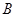 学科不合格人数 学科不合格人数 |
20 |
30 |
50 |
| 合计 |
60 |
50 |
110 |
(1)据此表格资料,你认为有多大把握认为“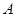 学科合格”与“
学科合格”与“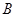 学科合格”有关;
学科合格”有关;
(2)从“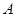 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“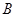 学科合格”的人数为
学科合格”的人数为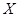 ,求
,求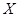 的数学期望.
的数学期望.
附公式与表: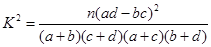
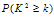 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
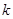 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| |
偏重 |
不偏重 |
合计 |
| 偏高 |
|
|
|
| 不偏高 |
|
|
|
| 合计 |
|
|
|
(2)请问该校17至18周岁的男生身高与体重是否有关?
对于有线性相关关系的变量x,y,测得一组数据如下表:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
20 |
40 |
60 |
70 |
80 |
根据上表得它们的回归直线方程为 ,据此模型来预 测当x=20时,y的估计值为
,据此模型来预 测当x=20时,y的估计值为
对于一组数据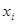 (
(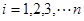 ),如果将它们改变为
),如果将它们改变为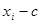 (
(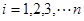 ),其中
),其中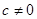 ,下列结论正确的是( )
,下列结论正确的是( )
| A.平均数与方差均不变 | B.平均数变了,而方差保持不变 |
| C.平均数不变,而方差变了 | D.平均数与方差均发生了变化 |
下列对一组数据的分析,不正确的说法是
| A.数据极差越小,样本数据分布越集中、稳定 |
| B.数据平均数越小,样本数据分布越集中、稳定 |
| C.数据标准差越小,样本数据分布越集中、稳定 |
| D.数据方差越小,样本数据分布越集中、稳定 |
已知二次函数 的x与y的部分对应值如下表:
的x与y的部分对应值如下表:
| x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| y |
11 |
|
1 |
-1 |
-1 |
1 |
5 |
且方程 的两根分别为
的两根分别为 、
、 ,下面说法错误的是( ) .
,下面说法错误的是( ) .
A. B.
B.
C.当 时,
时, D.当
D.当 时,
时, 有最小值
有最小值
第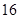 届亚运会于
届亚运会于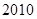 年
年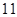 月
月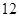 日至
日至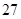 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了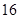 名男志愿者和
名男志愿者和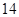 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有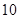 人和
人和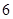 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下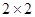 列联表:
列联表:
| |
喜爱运动 |
不喜爱运动 |
总计 |
| 男 |
10 |
|
16 |
| 女 |
6 |
|
14 |
| 总计 |
|
|
30 |
(2)能否在犯错误的概率不超过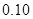 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有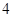 人会外语),抽取
人会外语),抽取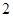 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中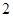 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=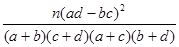
| P(K2≥k) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
某学生四次模拟考试时,其英语作文的扣分情况如下表:
考试次数 |
1 |
2 |
3 |
4 |
所减分数 |
4.5 |
4 |
3 |
2.5 |
显然所扣分数 与模拟考试次数
与模拟考试次数 之间有较好的线性相关关系,则其线性回归方程为( )
之间有较好的线性相关关系,则其线性回归方程为( )
A. B.
B. C.
C. D.
D.
为了调查胃病是否与生活规律有关,调查某地540名40岁以上的人得结果如下:
| |
患胃病 |
未患胃病 |
合计 |
| 生活不规律 |
60 |
260 |
320 |
| 生活有规律 |
20 |
200 |
220 |
| 合计 |
80 |
460 |
540 |
根据以上数据回答40岁以上的人患胃病与生活规律有关吗?
在某次测验中,有6位同学的平均成绩为75分.用 表示编号为
表示编号为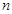
 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号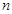 |
1 |
2 |
3 |
4 |
5 |
成绩 |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)求线性回归方程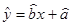 所表示的直线必经过的点;
所表示的直线必经过的点;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程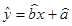 ;
;
并预测生产1000吨甲产品的生产能耗多少吨标准煤?
(参考: )
)
工人月工资(元)依劳动产值(千元)变化的回归直线方程为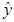 =60+90x,下列判断正确的是( )
=60+90x,下列判断正确的是( )
| A.劳动产值为1 000元时,工资为50元 |
| B.劳动产值提高1 000元时,工资提高150元 |
| C.劳动产值提高1 000元时,工资提高90元 |
| D.劳动产值为1 000元时,工资为90元 |
试题篮
()