某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了500名电视观众,相关的数据如下表所示:
 |
文艺节目 |
新闻节目 |
总计 |
| 大于40岁 |
40 |
30 |
70 |
| 20至40岁 |
160 |
270 |
430 |
| 总计 |
200 |
300 |
500 |
下列说法最准确的是 ( )
| A.有99%的把握认为收看不同节目类型的观众 与年龄有关 |
| B.有95%的把握认为收看不同节目类型的观众 与年龄有关 |
| C.有99%的把握认为收看不同节目类型的观众 与年龄无关 |
| D.有95%的把握认为收看不同节目类型的观众 与年龄无关 |
(参考公式: )
)
为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如下左图),已知图中从左到右的前3个小组的频率比为1:2:3,第2小组的频数为1 2,则抽取的男生人数是 。
2,则抽取的男生人数是 。
随机抽查某中学高三年级100名学生的视力情况,得其频率分布直方图如右图所示。已知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生人数为 人。
某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),
[98,100),[100,102),[102,104),[104,106], 已知样本中产品净重小于100克的个数是36,则样本中净重不小于100克并且小于104克的产品的个数是
| A.90 | B.75 | C.66 | D.45 |

统计某校1000名学生水平 测试成绩,得到样频率分布直方图如图所示,若满分为100分,规
测试成绩,得到样频率分布直方图如图所示,若满分为100分,规 定不低于60分为及格,则及格率是 ( )
定不低于60分为及格,则及格率是 ( )
| A.20% | B.25% |
| C.6% | D.80% |

(本小题满分12分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列 的前六项.
的前六项.
(I)求等比数列 的通项公式;
的通项公式;
(II)求等差数列 的通项公式;
的通项公式;
(III) 若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率 的大小.
的大小.
(本小题满分12分)某学校共有高一、高二、高三学生 名,各年级男、女生人数如下图:
名,各年级男、女生人数如下图:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0. 19.
(Ⅰ)求 的值;
的值;
(Ⅱ)现用分层抽样的方法在全校抽取 名学生,问应在高三年级抽取多少名?
名学生,问应在高三年级抽取多少名?
(Ⅲ)已知 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.
为了解一片经济树林的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出样本的频率分布直方图如图所示.那么在这100株树木中,底部周
长小于110cm的株数n 是 ( )
是 ( )
| A.30 | B.60 |
| C.70 | D.80 |

某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
15 |
① |
| 第2组 |
 |
② |
0.35 |
| 第3组 |
 |
20 |
0.20 |
| 第4组 |
 |
20 |
0.20 |
| 第5组 |
 |
10 |
0.10 |
| 合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
某地为了了解地区10000户家庭的用电情况,
采用分层抽样的方法抽取了500户家庭的月均
用电量,并根据这500户家庭的月均用电量画
|
出频率分布直方图(如图),则该地区10000户
家庭中月均用电度数在[70,80]的家庭大约有 户.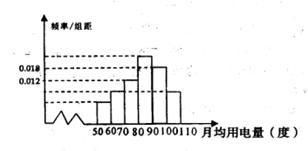
为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如右),那么在这100株树木中,底部周长小于110cm的株数是 .
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
, ,
, ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
⑴求 ;
;
⑵工厂规定从各组中任选1人进行再培训,则选取5人不在同一组的概率是多少?
试题篮
()