(本小题满分12分)
NBA总决赛采用“7场4胜制”,由于NBA有特殊的政策和规则,能进入决赛的球队实力都较强,因此可以认为,两个队在每一场比赛中取胜的概率相等。根据不完全统计,主办一场决赛,每一方组织者有望通过出售电视转播权、门票及零售商品、停车费、广告费等收入获取收益2000万美元(1)求比赛场数 的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
某班50名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].从样本成绩不低于80分的学生中随机选取2人,这2人中成绩在90分以上(含90分)的人数为ξ,则ξ的数学期望为( )
A. |
B. |
C. |
D. |
设 ,随机变量 取值 、 、 、 、 的概率均为0.2,随机变量 取值 、 、 、 、 的概率也为0.2.若记 、 分别为 、 的方差,则()
| A. | |
| B. | |
| C. | |
| D. | 与 的大小关系与 、 、 、 的取值有关 |
以每束1.6元价格处理.根据前五年销售情况预测,节日期间这种鲜花的需求量X服从如下表所示的分布:
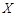 |
200 |
300 |
400 |
500 |
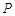 |
0.20 |
0.35 |
0.30 |
0.15 |
若进这种鲜花500束,则利润的均值为( )
A.706元 B.690元 C.754元 D.720元
(理)抛掷两个骰子,至少有一个4点或5点出现时,就说这些试验成功,则在10次试验中,成功次数ξ的期望是( )
A. |
B. |
C. |
D. |
从1,2,3,4,5中选3个数,用ξ表示这3个数中最大的一个,则E(ξ)=( )
| A.3 | B.4.5 | C.5 | D.6 |
一篮球运动员投篮一次得3分的概率为 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为 ,
,
其中 ,
, ,
, ,且无其它得分情况。已知他投篮一次得分的数学期望为1,则
,且无其它得分情况。已知他投篮一次得分的数学期望为1,则

的最大值是( )
A. |
B. |
C. |
D. |
在某次测量中得到的 样本数据如下:
样本数据如下: .若
.若 样本恰好是
样本恰好是 样本每个数据都加
样本每个数据都加 后所得数据,则
后所得数据,则 两样本的下列数字特征对应相同的是
两样本的下列数字特征对应相同的是
| A.众数 | B.平均数 | C.中位数 | D.标准差 |
签盒中有编号为1、2、3、4、5、6的六支签,从中任意取3支,设X为这3支签的号码之中最大的一个,则X的数学期望为( )
| A.5 | B.5.25 | C.5.8 | D.4.6 |
在“信阳市中学生歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )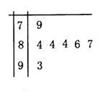
A.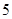 和 和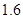 |
B. 和 和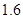 |
C. 和 和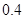 |
D.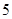 和 和 |
甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为 ,且各局胜负相互独立,则比赛停止时已打局数
,且各局胜负相互独立,则比赛停止时已打局数 的期望
的期望 为( )
为( )
A. |
B. |
C. |
D. |
利用下列盈利表中的数据进行决策,应选择的方案是( )
| A.A1 | B.A2 | C.A3 | D.A4 |
试题篮
()