高中数学随机思想的发展解答题

佛山某学校的场室统一使用“佛山照明”的一种灯管，已知这种灯管使用寿命（单位：月）服从正态分布，且使用寿命不少于个月的概率为，使用寿命不少于个月的概率为.
（1）求这种灯管的平均使用寿命；
（2）假设一间功能室一次性换上支这种新灯管，使用个月时进行一次检查，将已经损坏的灯管换下（中途不更换），求至少两支灯管需要更换的概率.

人寿保险中（某一年龄段），在一年的保险期内，每个被保险人需交纳保费a元，被保险人意外死亡则保险公司赔付3万元，出现非意外死亡则赔付1万元。经统计此年龄段一年内意外死亡的概率是p₁，非意外死亡的概率为p₂，则a需满足什么条件，保险公司才可能盈利.

某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

(1)分别求第3，4，5组的频率；
(2)若该校决定在笔试成绩较高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，
(ⅰ)已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙恰有一人进入第二轮面试的概率；
(ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试，设第4组中有名学生被考官L面试，求的分布列和数学期望．

某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响．
（I）任选1名下岗人员，求该人参加过培训的概率；
（II）任选3名下岗人员，记为3人中参加过培训的人数，求的分布列和期望．

（本小题共13分）某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在地区附近有A，B，C三家社区医院，并且他们的选择是相互独立的．
（Ⅰ）求甲、乙两人都选择A社区医院的概率；
（Ⅱ）求甲、乙两人不选择同一家社区医院的概率；
（Ⅲ）设4名参加保险人员中选择A社区医院的人数为ξ，求ξ的分布列和数学期望．

已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑球．现从甲、乙两个盒内各任取2个球．
（Ⅰ）求取出的4个球均为黑球的概率；
（Ⅱ）求取出的4个球中恰有1个红球的概率；
（Ⅲ）设为取出的4个球中红球的个数，求的分布列和数学期望．

在一个盒子中，放有标号分别为1,2,3的三张卡片，现从这个盒子中有放回地先后抽取两张卡片，并设它们的标号分别为x，y，记ξ＝|x－2|＋|y－x|.
(1)求随机变量ξ的范围；(2)分别求出ξ取不同值时的概率；

某商场为吸引顾客消费推出一项优惠活动.活动规则如下：消费额每满100元可转动如图所示的圆盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置. 若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券. 例如：消费218元，可转动圆盘2次，所获得的返券金额是两次金额之和.
（1）若某位顾客消费128元，求返券金额不低于30元的概率；
（2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记
为（元）.求随机变量的分布列和数学期望.

（本小题满分12分）某班同学利用国庆节进行社会实践，对 [25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：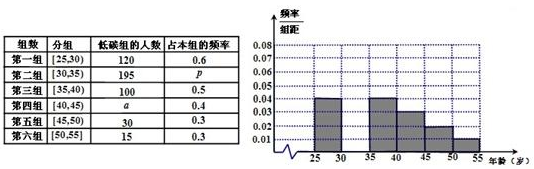

（1）补全频率分布直方图并求n、a、p的值；
（2）从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和期望E（X）．

（本小题满分12分）一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为l，2，3，4，5：4个白球编号分别为1，2，3，4，从袋中任意取出3个球．
（Ⅰ）求取出的3个球编号都不相同的概率；
（Ⅱ）记X为取出的3个球中编号的最大值，求X的分布列与数学期望

近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重，大气污染可引起心悸、呼吸困难等心肺疾病．为了解某市心肺疾病是否与性别有关，在某医院随机对入院的50人进行了问卷调查得到了如下的列联表：

	患心肺疾病	不患心肺疾病	合计
男		5
女	10
合计			50

 
已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为．
(1)请将上面的列联表补充完整；
(2)是否有99．5%的把握认为患心肺疾病与性别有关？说明你的理由；
临界值表供参考：

P(K^2≥k)	0．15	0．10	0．05	0．025	0．010	0．005	0．001
k	2．072	2．706	3．841	5．024	6．635	7．879	10．828

 
参考公式：其中

2013年4月20日8时02分四川省雅安市芦山县（北纬30.3,东经103.0）发生7.0级地震。一方有难，八方支援，重庆众多医务工作者和志愿者加入了抗灾救援行动。其中重庆某医院外科派出由5名骨干医生组成的救援小组，奔赴受灾第一线参与救援。现将这5名医生分别随机分配到受灾最严重的芦山、宝山、天全三县中的某一个。
（1）求每个县至少分配到一名医生的概率。
（2）若将随机分配到芦山县的人数记为，求随机变量的分布列，期望和方差。

（本小题满分12分）
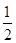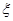甲，乙，丙三位学生独立地解同一道题，甲做对的概率为，乙，丙做对的概率分别为， (＞)，且三位学生是否做对相互独立.记为这三位学生中做对该题的人数，其分布列为：

	0	1	2	3

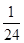（1) 求至少有一位学生做对该题的概率；
（2) 求，的值；
（3) 求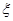的数学期望.

某学校设计了一个实验学科的考查方案：考生从6道备选题中一次性抽取3道题，规定至少正确完成其中2道题便可通过，已知6道备选题中考生甲有4道能正确完成，2道不能完成；考生乙正确完成每道题的概率都是，且每题正确完成与否互不影响．
⑴求甲正确完成的题数的分布列及期望；求乙正确完成的题数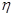的分布列及期望；
⑵请用统计知识分析比较两名考生这门学科的水平．

某寻呼台共有客户3000人，若寻呼台准备了100份小礼品，邀请客户在指定时间来领取．假设任一客户去领奖的概率为4％．问：寻呼台能否向每一位顾客都发出奖邀请？若能使每一位领奖人都得到礼品，寻呼台至少应准备多少礼品？