下列说法错误的是 ( )
A.命题:“已知f(x)是R上的增函数,若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”的逆否命题为真命题 |
B.命题p:“∃x∈R,使得x2+x+1<0”,则 p:“∀x∈R,均有x2+x+1≥0” |
| C.若p且q为假命题,则p、q均为假命题 | |
| D.“x>1”是“|x|>1”的充分不必要条件 |
关于数列{an}有以下命题,其中错误的命题为 ( )
A.若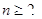 且 且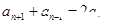 ,则 ,则 是等差数列 是等差数列 |
B.设数列 的前 的前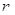 项和为 项和为 ,且 ,且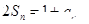 ,则数列 ,则数列 的通项 的通项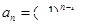 |
C.若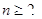 且 且 ,则 ,则 是等比数列 是等比数列 |
D.若 是等比数列,且 是等比数列,且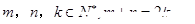 ,则 ,则 |
对于函数① ,②
,② ,③
,③ ,
,
判断如下两个命题的真假:
命题甲: 在区间
在区间 上是增函数;
上是增函数;
命题乙: 在区间
在区间 上恰有两个零点
上恰有两个零点 ,且
,且 .
.
能使命题甲、乙均为真的函数的序号是
| A.① | B.② | C.①③ | D.①② |
设 ,
, ,
, 是三个不重合的平面,
是三个不重合的平面, 是直线,给出下列命题
是直线,给出下列命题
①若 ,
, ,则
,则 ; ②若
; ②若 上两点到
上两点到 的距离相等,则
的距离相等,则 ;
;
③若 ,
, ,则
,则 ; ④若
; ④若 ,
, ,且
,且 ,则
,则 .
.
其中正确的命题是
| A.①② | B.②③ | C.②④ | D.③④ |
已知 为不重合的两个平面,直线
为不重合的两个平面,直线 那么“
那么“ ”是“
”是“ ”( )
”( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知空间两条不同的直线m,n和两个不同的平面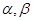 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若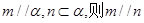 |
B.若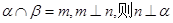 |
C.若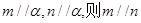 |
D.若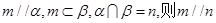 |
设 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不重合的平面,给定下列四个命题,其中真命题的是 ( )
是两个不重合的平面,给定下列四个命题,其中真命题的是 ( )
①若 ,
, ,则
,则
 ; ②若
; ②若 ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ; ④若
; ④若 ,
, ,
, 则
则 。
。
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
连结球面上两点的线段称为球的弦.半径为4的球的两条弦 的长度分别等于2
的长度分别等于2 、4
、4 ,
, 分别为
分别为 的中点,每条弦的两端都在球面上运动,有下列四个命题:
的中点,每条弦的两端都在球面上运动,有下列四个命题:
①弦 可能相交于点
可能相交于点 ,②弦
,②弦 可能相交于点
可能相交于点 ,③
,③ 的最大值为5
的最大值为5
④ 的最小值为l.
的最小值为l.
其中真命题的个数为
| A.1个 | B.2个 | C.3个 | D.4个 |
对于函数① ,②
,② ,③
,③ ,判断如下两个命题的真假:
,判断如下两个命题的真假:
命题甲: 在区间
在区间 上是增函数;
上是增函数;
命题乙: 在区间
在区间 上恰有两个零点
上恰有两个零点 ,且
,且 .能使命题甲、乙均为真的函数的序号是
.能使命题甲、乙均为真的函数的序号是
| A.① | B.② | C.①③ | D.①② |
若 、
、 为两条不重合的直线,
为两条不重合的直线, 、
、 为两个不重合的平面,则下列命题中的真命题个数是( )
为两个不重合的平面,则下列命题中的真命题个数是( )
①若 、
、 都平行于平面
都平行于平面 ,则
,则 、
、 一定不是相交直线;
一定不是相交直线;
②若 、
、 都垂直于平面
都垂直于平面 ,则
,则 、
、 一定是平行直线;
一定是平行直线;
③已知 、
、 互相垂直,
互相垂直, 、
、 互相垂直,若
互相垂直,若 ,则
,则 ;
;
④ 、
、 在平面
在平面 内的射影互相垂直,则
内的射影互相垂直,则 、
、 互相垂直.
互相垂直.
| A.1 | B.2 | C.3 | D.4 |
给出定义:若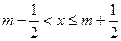 (其中m为整数),则m 叫做离实数x最近的整数,记作
(其中m为整数),则m 叫做离实数x最近的整数,记作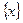 =" m." 在此基础上给出下列关于函数
=" m." 在此基础上给出下列关于函数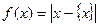 的四个命题:
的四个命题:
①函数y=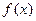 的定义域为R,值域为
的定义域为R,值域为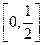 ;
;
②函数y=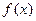 的图像关于直线
的图像关于直线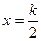 (
(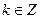 )对称;
)对称;
③函数y=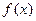 是周期函数,最小正周期为1;
是周期函数,最小正周期为1;
④函数y=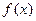 在
在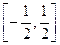 上是增函数.
上是增函数.
其中正确的命题的序号是
| A.① | B.②③ | C.①②③ | D.①④ |
已知直线a,b与平面α,给出下列四个命题:
①若a∥b,b α,则a∥α; ②若a∥α,b
α,则a∥α; ②若a∥α,b α,则a∥b;
α,则a∥b;
③若a∥α,b∥α,则a∥b; ④若a⊥α,b∥α,则a⊥b.
其中正确命题的个数是
| A.1 | B.2 | C.3 | D.4 |
已知直线 、
、 ,平面
,平面 、
、 ,给出下列命题:
,给出下列命题:
①若 ,且
,且 ,则
,则 ②若
②若 ,且
,且 ,则
,则
③若 ,且
,且 ,则
,则 ④若
④若 ,且
,且 ,则
,则
其中正确的命题的个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
关于直线a, b, l以及平面M,N.下列命题中正确的是
| A.若a∥M, b∥M 则a∥b |
| B.若a∥M, b⊥a则b⊥M |
C.若a M, b M, b M, 且l⊥a, l⊥b 则l⊥M M, 且l⊥a, l⊥b 则l⊥M |
| D.若a⊥M, a∥N 则 N⊥M |
试题篮
()