已知定义在 上的函数f(x)同时满足下列三个条件:
上的函数f(x)同时满足下列三个条件:
①f(3)=﹣1;②对任意x、y∈ 都有f(xy)=f(x)+f(y);③x>1时,f(x)<0.
都有f(xy)=f(x)+f(y);③x>1时,f(x)<0.
(1)求f(9)、 的值;
的值;
(2)证明:函数f(x)在 上为减函数;
上为减函数;
(3)解关于x的不等式f(6x)<f(x﹣1)﹣2.
已知集合A={x|x2+ax﹣12=0},B={x|x2+bx+c=0},且A≠B,A∩B={﹣3},A∪B={﹣3,1,4},求实数a,b,c的值.
已知极坐标系的极点与直角坐标系的原点重合,极轴与 轴的正半轴重合.若直线
轴的正半轴重合.若直线 的极坐标方程为
的极坐标方程为 .
.
(1)把直线 的极坐标方程化为直角坐标系方程;
的极坐标方程化为直角坐标系方程;
(2)已知 为椭圆
为椭圆 上一点,求
上一点,求 到直线
到直线 的距离的最大值。
的距离的最大值。
已知函数f(x)=xln(1+x)-a(x+1),其中a为实常数.
(1)当x∈[1,+∞)时,f′(x)>0恒成立,求a的取值范围;
(2)求函数g(x)=f′(x)- 的单调区间.
的单调区间.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如下图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4.第一小组的频数是5.
(1)求第四小组的频率和参加这次测试的学生人数;
(2)在这次测试中,学生跳绳次数的中位数落在第几小组内?
(3)参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
已知椭圆 的上顶点为(0,2),且离心率为
的上顶点为(0,2),且离心率为 ,
,
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:过圆 上一点
上一点 的切线方程为
的切线方程为 ;
;
(Ⅲ)从椭圆C上一点P向圆 上向引两条切线,切点为A,B,当直线AB分别与x轴、y轴交于M,N两点时,求
上向引两条切线,切点为A,B,当直线AB分别与x轴、y轴交于M,N两点时,求 的最小值.
的最小值.
已知两条直线l1:ax-by+4=0,l2:(a-1)x+y+b=0,直线l1过点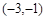 ,并且直线l1与直线l2垂直.求满足条件的a,b的值.
,并且直线l1与直线l2垂直.求满足条件的a,b的值.
试题篮
()