(本小题满分10分)选修4-4:坐标系与参数方程已知曲线 :
: (
( 为参数),
为参数), :
: (
( 为参数).
为参数).
(Ⅰ)化 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若 上的点
上的点 对应的参数为
对应的参数为 ,
, 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
( 为参数)距离的最小值.
为参数)距离的最小值.
(本小题满分12分)已知 是公差为
是公差为 的等差数列,它的前
的等差数列,它的前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求公差 的值;
的值;
(Ⅱ)若 ,
, 是数列
是数列 的前
的前 项和,不等式
项和,不等式 对所有的
对所有的 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.
(本小题满分12分)已知函数 .
.
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)若对于任意 ,不等式
,不等式 恒成立,求正实数
恒成立,求正实数 的取值范围.
的取值范围.
(本小题满分12分) 在 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 。
。
(1)求角 的大小;
的大小;
(2)若 ,
, 的面积为
的面积为 ,求
,求 的值。
的值。
(本小题满分12分) 设 为数列
为数列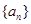 的前
的前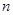 项和,且对任意
项和,且对任意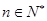 时,点
时,点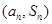 都在函数
都在函数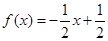 的图象上。
的图象上。
(1)求数列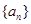 的通项公式;
的通项公式;
(2)设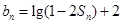 ,求数列
,求数列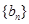 的前
的前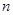 项和
项和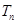 的最大值。
的最大值。
(本小题满分12分) 某校校庆,各界校友纷至沓来,某班共来了 位校友(
位校友(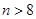 且
且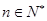 ),其中女校友
),其中女校友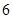 位,组委会对这
位,组委会对这 位校友登记制作了一份校友名单,现随机从中选出
位校友登记制作了一份校友名单,现随机从中选出 位校友代表,若选出的
位校友代表,若选出的 位校友代表是一男一女,则称为“友情搭档”。
位校友代表是一男一女,则称为“友情搭档”。
(1)若随机选出的 位校友代表为“友情搭档”的概率不小于
位校友代表为“友情搭档”的概率不小于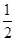 ,求
,求 的最大值;
的最大值;
(2)当 时,设选出的
时,设选出的 位校友代表中女校友人数为
位校友代表中女校友人数为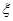 ,求
,求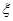 的分布列和均值。
的分布列和均值。
(本小题满分12分)在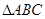 中,角
中,角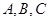 的对边分别是
的对边分别是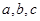 ,若
,若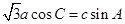 。
。
(1)求角 的大小;
的大小;
(2)若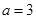 ,
,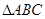 的面积为
的面积为 ,求
,求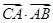 的值。
的值。
试题篮
()