某纺织厂订购一批棉花,其各种长度的纤维所占的比例如下表所示:
| 纤维长度(厘米) |
3 |
5 |
6 |
| 所占的比例(%) |
25 |
40 |
35 |
(1)请估计这批棉花纤维的平均长度与方差;
(2)如果规定这批棉花纤维的平均长度为4.90厘米,方差不超过1.200,两者允许误差均不超过0.10视为合格产品.请你估计这批棉花的质量是否合格?
某班进行个人投篮比赛,受污损的下表记录了在规定时间内投进n个球的人数分布情况:
| 进球数n |
0 |
1 |
2 |
3 |
4 |
5 |
| 投进n个球的人数 |
1 |
2 |
7 |
|
|
2 |
同时,已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下人平均每人投进2.5个球.那么投进3个球和4个球的各有多少人?
某医院为了了解病人每分钟呼吸次数,对20名病人进行测量,记录结果如下:
12,20,16,18,20,28,23,16,15,18,20,24,18,21,18,19,18,31,18,13,
求这组数据的平均数,中位数,众数.
已知空间直角坐标系O﹣xyz中的点A(1,1,1),平面α过点A且与直线OA垂直,动点P(x,y,z)是平面α内的任一点.
(1)求点P的坐标满足的条件;
(2)求平面α与坐标平面围成的几何体的体积.
在空间直角坐标系中,解答下列各题:
(1)在x轴上求一点P,使它与点P0(4,1,2)的距离为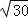 ;
;
(2)在xOy平面内的直线x+y=1上确定一点M,使它到点N(6,5,1)的距离最小.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.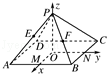
集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)为集合A的同一种分拆,则集合A={a,b,c}的不同分拆种数为多少?
某年级先后举办了数学、历史、音乐的讲座,其中有75人听了数学讲座,68人听了历史讲座,61人听了音乐讲座,17人同时听了数学、历史讲座,12人同时听了数学、音乐讲座,9人同时听了历史、音乐讲座,还有6人听了全部讲座.求听讲座的人数.
已知a∈R,b∈R,A={2,4,x2﹣5x+9},B={3,x2+ax+a},C={x2+(a+1)x﹣3,1}:求
(1)A={2,3,4}的x值;
(2)使2∈B,B⊊A,求a,x的值;
(3)使B=C的a,x的值.
试题篮
()