设计如图所示一水渠,它的横截面曲线是抛物线形, 宽2m,渠
宽2m,渠 深为1.5m,水面EF距AB为0.5m. (1)求截面图中水面宽度;
深为1.5m,水面EF距AB为0.5m. (1)求截面图中水面宽度; (2)由于情况有变,现要将此水渠改造为横截面是等腰梯形,要求渠深不变,不准往回填土,只准挖土,试求截面梯形的下边长为多大时,才能使所挖的土最少?
(2)由于情况有变,现要将此水渠改造为横截面是等腰梯形,要求渠深不变,不准往回填土,只准挖土,试求截面梯形的下边长为多大时,才能使所挖的土最少?
现有流量均为300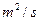 的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2
的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2 和0.2
和0.2 .假设从汇合处开始,沿岸设有若干个观测点,两股水流在流经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交换100
.假设从汇合处开始,沿岸设有若干个观测点,两股水流在流经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交换100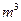 的水量,即从A股流入B股100
的水量,即从A股流入B股100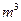 水,经混合后,又从B股流入A股100
水,经混合后,又从B股流入A股100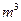 水并混合.问:从第几个观测点开始,两股河水的含沙量之差小于0.01
水并混合.问:从第几个观测点开始,两股河水的含沙量之差小于0.01 (不考虑泥沙沉淀)?
(不考虑泥沙沉淀)?
某观测站C在城A的南20˚西的方向上,由A城出发有一条公路,走向是南40˚东,在C处测得距C为31千米的公路上B处有一人正沿公路向A城走去,走了20千米后,到达D处,此时C、D间距离为21千米,问这人还需走多少千米到达A城?
某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
(1)写出第一次服药后y与t之间的函数关系式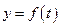 ;
;
(2)据进一步测定:每毫升血液中含药量不少于0.25
微克时,治疗有效.
①求服药一次后治疗有效的时间是多长?
②当 时,第二次服药,问
时,第二次服药,问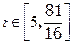 时药效能否持续?
时药效能否持续?
某校有教职员工150人,为了丰富教工的课余生活,每天定时开放健身房和娱乐室.据调查统计,每次去健身房的人有10%下次去娱乐室,而在娱乐室的人有20%下次去健身房.请问,随着时间的推移,去健身房的人数能否趋于稳定?
(本小题满分12分)
设进入某商场的每一位顾客购买甲种商品的概率为 ,购买乙种商品的概率为
,购买乙种商品的概率为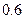 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记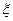 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求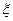 的分布列及期望。
的分布列及期望。
(本小题满分13分)
如图,椭圆C:  的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线
的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线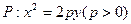 的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且
的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且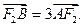
(I)求证:切线l的斜率为定值
|
(Ⅱ)设抛物线P与直线l切于点E,若△OEF2面积为1,求椭圆C和抛物线P的方程。
(本小题满分13分)
已知函数
(I)求函数 的单调区间;
的单调区间;
(II)若 有三个交点,求m的取值范围(其中自然对数的底数e为无理数且
有三个交点,求m的取值范围(其中自然对数的底数e为无理数且 )
)
(本小题满分14分)
已知函数 的反函数为
的反函数为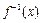 ,数列
,数列 和
和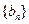 满足:
满足: ,
, ;函数
;函数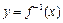 的图象在点
的图象在点 处的切线在y轴上的截距为
处的切线在y轴上的截距为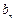 .
.
(1)求数列{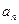 }的通项公式;
}的通项公式;
(2)若数列 的项仅
的项仅 最小,求
最小,求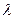 的取值范围;
的取值范围;
(3)令函数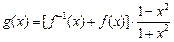 ,
,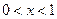 ,数列
,数列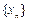 满足:
满足: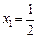 ,
,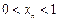 ,且
,且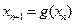 ,其中
,其中 .证明:
.证明: .
.
(本小题满分14分)
已知椭圆 过点
过点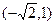 ,长轴长为
,长轴长为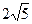 ,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.
,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.
(1)求椭圆的方程;
(2)若线段AB中点的横坐标是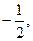 求直线l的斜率;
求直线l的斜率;
(3)在x轴上是否存在点M,使 是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由.
是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由.
(本小题满分14分)
设函数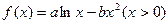
(1)若函数 在x=1处与直线
在x=1处与直线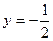 相切
相切
①求实数a,b的值;
②求函数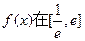 上的最大值.
上的最大值.
(2)当b=0时,若不等式 对所有的
对所有的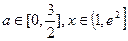 都成立,求
都成立,求 实数m的取值范围.
实数m的取值范围.
试题篮
()