已知抛物线 的焦点为 , 点 在 上, 且 , 则 的横坐标是 ; 作 轴于 , 则 的面积为 .
已知平面向量 满足 .记向量 在 方向上的投影分别为x,y, 在 方向上的投影为z,则 的最小值为___________.
已知椭圆
,焦点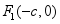 ,
,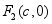 ,若过
的直线和圆
相切,与椭圆在第一象限交于点P,且
轴,则该直线的斜率是___________,椭圆的离心率是___________.
,若过
的直线和圆
相切,与椭圆在第一象限交于点P,且
轴,则该直线的斜率是___________,椭圆的离心率是___________.
袋中有4个红球m个黄球,n个绿球.现从中任取两个球,记取出的红球数为 ,若取出的两个球都是红球的概率为 ,一红一黄的概率为 ,则 ___________, ___________.
我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别是3,4,记大正方形的面积为 ,小正方形的面积为 ,则 ___________.

已知函数 ,函数 的图象在点 和点 的两条切线互相垂直,且分别交y轴于M,N两点,则 取值范围是_______.
试题篮
()