质量为m的小球,从离桌面以上高为H的地方以初速度v0竖直向上抛出,桌面离地面高为h,设桌面处物体重力势能为零,空气阻力不计,那么,小球落地时的机械能为
A.mgh+ |
B. |
C.mg(H+h) + |
D.mg(H +h) |
在地面上以初速度 竖直上抛一物体A后,又以初速度
竖直上抛一物体A后,又以初速度 在同一地点竖直上抛另一个物体B,若要使两物体能在空中相遇,则两物体抛出的时间间隔
在同一地点竖直上抛另一个物体B,若要使两物体能在空中相遇,则两物体抛出的时间间隔 必须满足的条件是(不计空气阻力):
必须满足的条件是(不计空气阻力):
A. |
B. |
C. |
D. |
在竖直的井底,将一物块以11 m/s的速度竖直的向上抛出,物体冲过井口时被人接住,在被人接住前1s内物体的位移是4 m,位移方向向上,不计空气阻力,g取10 m/s2,求:
(1)物体从抛出到被人接住所经历的时间;
(2)此竖直井的深度.
将小球从高塔边以 m/s的初速度竖直上抛,空气阻力忽略不计。重力加速度
m/s的初速度竖直上抛,空气阻力忽略不计。重力加速度 m/s2。求:
m/s2。求:
(1)经多长时间小球的速度大小为10m/s;
(2)经 s时,小球离抛出点的距离为多少。
s时,小球离抛出点的距离为多少。
在不计空气阻力的情况下,某物体以30m/s的初速度从地面竖直上抛,则(g取10m/s2)
( )
| A.前4s内物体的位移大小为50m |
| B.前4s内物体的平均速度大小为10m/s |
| C.第2s末到第4s末物体的平均速度为5m/s |
| D.第2s末到第4s内物体的速度改变量相同 |
近年来测重力加速度g值的一种方法叫“对称自由下落法”。具体做法是:将真空长直管沿竖直方向放置,自其中O点向上抛小球又落至原处所用时间为t2,在小球运动过程中经过比O点高h的B点,小球离开B点至又回到B点所用时间为t1,测得t1、t2、h,则重力加速度的表达式为( )
A. |
B. |
C. |
D. |
从地面上以初速度v0竖直上抛一质量为m的小球,若运动过程中受到的空气阻力与其速率成正比,小球运动的速率随时间变化的规律如图所示,t1时刻到达最高点,再落回地面,落地速率为v1,且落地前小球已经做匀速运动,则下列说法正确的是( )

| A.小球加速度在上升过程中逐渐减小,在下降过程也逐渐减小 |
B.小球抛出瞬间的加速度大小为(1+ )g )g |
| C.小球被抛出时的加速度值最大,到达最高点的加速度值最小 |
D.小球上升过程的平均速度小于 |
带电小球以一定的初速度 竖直向上抛出,能够达到的最大高度
竖直向上抛出,能够达到的最大高度 ;若加上水平方向的匀强磁场,且保持初速度仍为
;若加上水平方向的匀强磁场,且保持初速度仍为 ,小球上升的最大高度为
,小球上升的最大高度为 ,若加上水平方向的匀强电场,且保持初速度仍为
,若加上水平方向的匀强电场,且保持初速度仍为 ,小球上升的最大高度为
,小球上升的最大高度为 ,如图所示,不计空气阻力,则
,如图所示,不计空气阻力,则
A. |
B. |
C. |
D. |
从离地H高处自由释放小球a,同时在地面以速度v0竖直上抛另一小球b,有( )
A.若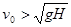 ,小球b在上升过程中与a球相遇 ,小球b在上升过程中与a球相遇 |
B.若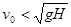 ,小球b在下落过程中肯定与a球相遇 ,小球b在下落过程中肯定与a球相遇 |
C.若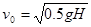 ,小球b和a肯定会在空中相遇 ,小球b和a肯定会在空中相遇 |
D.若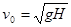 ,两球在空中相遇时b球速度为零 ,两球在空中相遇时b球速度为零 |
将一物体以20m/s的初速度竖直向上抛出,从抛出开始计时,当物体运动至抛出点上方15m处所经历的时间是( )
| A.1s | B.2s | C.3s | D.4s |
如图所示,离地面足够高处有一竖直的空管,管长为24m,M、N为空管的上、下两端,空管受到外力作用,由静止开始竖直向下做匀加速运动,加速度为2m/s2.同时在M处一个大小不计的小球沿管的轴线竖直上抛,小球只受重力,取g=10m/s2.求: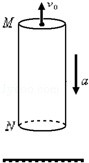
(1)若小球上抛的初速度为10m/s,经过多长时间从管的N端穿处?
(2)若此空管的N端距离地面64m高,欲使在空管到达地面时小球必须落到管内,在其他条件不变的前提下,求小球的初速度大小的范围?
某人在静止的湖面上竖直上抛一小铁球,小铁球上升到最高点后自由下落,穿过湖水并陷入湖底的淤泥中某一深度处.若不计空气阻力,取竖直向上为正方向,则最能反映小铁球运动过程的速度与时间关系的图象是 ( )
以一定的初速度竖直向上抛出一个小球,小球上升的最大高度为h,空气阻力的大小恒为F,则从抛出到落回到抛出点的过程中,空气阻力对小球做的功为: ( )
| A.0 | B.-Fh | C.Fh | D.-2Fh |
试题篮
()