物体在同一平面内受F1、F2、F3三个共点力的作用处于平衡状态,当把F3的方向在同平面内旋转60°时(F3大小不变,F1、F2大小方向都不变),则三力的合力大小为( )
| A.0 | B.F3 | C. F3 F3 |
D.2F3 |
如图,重为200牛的重物由ON、OM绳悬挂在天花板上,已知(ONM=60(,(OMN=30(,请画出受力分析图并求绳ON和绳OM受到的拉力的大小?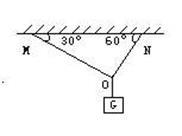
如图所示,质量M= 的木块A套在水平杆上,并用轻绳将木块:A与质量m=
的木块A套在水平杆上,并用轻绳将木块:A与质量m= 的小球相连。今用跟水平方向成α=30o角的力F=
的小球相连。今用跟水平方向成α=30o角的力F=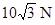 ,拉着球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取g=10m/s 2。求:
,拉着球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取g=10m/s 2。求:
(1)运动过程中轻绳与水平方向夹角θ;
(2)木块与水平杆间的动摩擦因数为μ。
如图所示,小娟、小明两人共提一桶水匀速前行。已知两人手臂对桶的拉力大小相等且为F,两人手臂间的夹角为θ,水和水桶总重为G,则下列说法中正确的是
| A.当θ=0°时,F=G | B.当θ为120°时,F=G |
| C.当θ=90°时,F=G | D.θ越大,F越大 |
不在同一直线上的两个共点力 和
和 的大小不同,夹角为
的大小不同,夹角为 ,它们的合力大小为F,则
,它们的合力大小为F,则
A.合力F可能沿 和 和 夹角的角平分线 夹角的角平分线 |
B.保持 和 和 的大小不变,夹角 的大小不变,夹角 增大,合力F一定减小 增大,合力F一定减小 |
C.保持夹角 不变,若 不变,若 和 和 中的一个减小,合力F一定减小 中的一个减小,合力F一定减小 |
D.保持夹角 不变, 不变, 和 和 同时增大一倍,合力F也增大一倍 同时增大一倍,合力F也增大一倍 |
如图所示,小球用细绳系住,绳的另一端固定与O点,现用水平力F缓慢的推动斜面体,小球在斜面上无摩擦地滑动,细绳始终处于直线状态,当小球升到接近斜面顶端时细绳接近水平,此过程中斜面对小球的支持力 以及绳对小球的拉力
以及绳对小球的拉力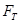 的变化情况是
的变化情况是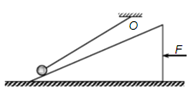
A. 保持不变, 保持不变,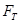 不断增大 不断增大 |
B. 不断增大, 不断增大,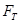 不断减小 不断减小 |
C. 保持不变, 保持不变,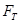 先增大后减小 先增大后减小 |
D. 不断增大, 不断增大,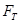 先减小后增大 先减小后增大 |
如图所示,光滑半球形容器固定在水平面上,O为球心,一质量为m的小滑块,在水平力F的作用静止与P点,设滑块所受支持力为 ,OP与水平方向的夹角为
,OP与水平方向的夹角为 ,下列关系正确的是
,下列关系正确的是
A. |
B. |
C.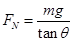 |
D.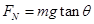 |
一物体以一定的初速度从斜面底端沿斜面向上运动,上升到最高点后又沿斜面滑下,某段时间的速度—时间图像如图所示,g=10m/s2,由此可知斜面倾角为( )

| A.300 | B.370 | C.530 | D.600 |
将力F分解成F1和F2,若已知F1的大小和F2与F的夹角θ(θ为锐角),则下列判断不正确的是( )
| A.当F1>Fsinθ时,有两解 |
| B.当F1=Fsinθ时,一解 |
| C.当Fsinθ<F1<F时,有两解 |
| D.当F1<Fsinθ时,无解 |
如图所示,开口向下的“┍┑”形框架,两侧竖直杆光滑固定,上面水平横杆中点固定一定滑轮,两侧杆上套着的两滑块用轻绳绕过定滑轮相连,并处于静止状态,此时连接滑块A的绳与水平方向夹角为θ,连接滑块B的绳与水平方向的夹角为2θ,则A、B两滑块的质量之比为( )
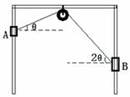
A.2sinθ:1 B.2cosθ:1 C.1:2cosθ D.1:2sinθ
现在城市的滑板运动非常流行,在水平地面上一名滑板运动员双脚站在滑板上以一定速度向前滑行,在横杆前起跳并越过杆,从而使人与滑板分别从杆的上下通过,如图所示.假设人和滑板运动过程中受到的各种阻力忽略不计,运动员能顺利完成该动作,最终仍落在滑板原来的位置上,要使这个表演成功,运动员除了跳起的高度足够外,在起跳时双脚对滑板作用力的合力方向应该
| A.竖直向上 | B.向下适当偏后 |
| C.竖直向下 | D.向上适当偏前 |
如图所示,一个菱形框架绕着过对角线的竖直轴匀速转动,在两条边上各有一个质量相等的小球套在上面,整个过程小球相对框架没有发生滑动,A与B到轴的距离相等,则下列说法正确的是
A.框架对A的弹力方向可能垂直框架向下
B.框架对B的弹力方向只能垂直框架向上
C.A与框架间可能没有摩擦力
D.A、B两球所受的合力大小相等
试题篮
()