如图所示，质量m =" 23" kg的物体静止于水平地面的A处，A.B间距L =" 24" m。用与水平方向成θ = 37°的力F斜向上拉此物体，作用一段时间后撤去该力，再经t0 =" 4" s物体刚好停于B处。已知物体与地面间的动摩擦因数μ = 0.2，sin37o = 0.6，取g =" 10" m/s2。
试分析：
(1)撤去拉力的瞬间，物体的速度v的大小为多少？
(2)作用在物体上的倾斜拉力F的大小为多少？
如图所示将重为G的物体A放在倾角为37°的斜面上，A与斜面间的摩擦因数为0.1，那么对A施加一个可能多大的水平力，可使A物体保持静止状态？（设A物体受到的最大静摩擦力与滑动摩擦力大小相等，sin37°=0.6 cos37°=0.8）
如图所示横梁BC为水平轻杆，且B端用铰链固定在竖直墙上，轻绳AD拴接在C端，D端所挂物体质量M=10kg，g取10 m/s2，求：
(1)轻绳AC段的张力FAC的大小；
(2)轻杆BC对C端的支持力．
如图所示,质量为mB=14kg的木板B放在水平地面上,质量为mA=10kg的货箱A放在木板B上。一根轻绳一端拴在货箱上,另一端拴在地面上,绳绷紧时与水平面的夹角为θ=37°。已知货箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4。重力加速度g取10m/s2。现用水平力F将木板B从货箱A下面匀速抽出, (已知：sin37°=" 0.6" cos37°="0.8)" 试求：
(1)绳上张力T的大小。
(2)水平拉力F的大小。
如图所示，轻绳OA一端系于天花板上，与竖直方向的夹角为θ，水平轻绳OB的一端系于竖直墙上，O点挂一重物。当重物的重力为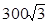
N时，水平绳OB的拉力为300N，求：
（1）θ角的大小？
（2）此时绳OA的拉力是多大？
如图所示，用绳AC和BC吊起一重物，绳与竖直方向夹角分别为30°和60°，AC绳能承受的最大拉力为150N，而BC绳能承受的最大的拉力为100N，求物体最大重力不能超过多少？
如图所示,物体的质量为2 kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围．
如图所示，一质量为m=100kg的箱子静止在水平面上，与水平面间的动摩擦因素为μ=0.5。现对箱子施加一个与水平方向成θ=37°角的拉力，经t1=10s后撤去拉力，又经t2=1s箱子停下来。sin37°=0.6，cos37°=0.8，g＝10m/s2。求：
（1）拉力F大小；
（2）箱子在水平面上滑行的位移x。
将橡皮筋的一端固定在A点，另一端拴上两根细绳．每根细绳分别连着一个量程为5N，最小刻度为0.1N的弹簧测力计．沿着两个不同的方向拉弹簧测力计．当橡皮筋的活动端拉到O点时，两根细绳相互垂直，如图所示，这时弹簧测力计的读数可从图中读出．
（1）由图可读得两个相互垂直的拉力的大小分别为 N和 N．
（2）在方格纸上按作图法的要求画出这两个力及它们的合力．
（3）求其合力的大小．
如图所示，一足够长的固定光滑斜面倾角
=37°，两物块A、B的质量
1kg、
4kg。两物块之间的轻绳长L=0.5m，轻绳可承受的最大拉力为T=12N，对B施加一沿斜面向上的力 F，使A、B由静止开始一起向上运动，力F逐渐增大， g取10m/s2（sin37°=0.6，cos37°=0.8）。
（1）若某一时刻轻绳被拉断，求此时外力F的大小；
（2）若轻绳拉断瞬间A、B的速度为3m/s，绳断后保持外力F不变，求当A运动到最高点时，A、B之间的距离。
如下图所示，一个人用与水平方向成θ＝37°角的斜向下的推力F推一个重G＝200Ｎ的箱子匀速前进，箱子与地面间的动摩擦因数为μ＝0.5（sin370=0.6,cos370=0.8,g=10m/s2）。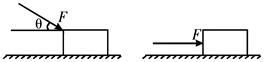
（1）求推力F的大小；
（2）若此人不改变推力Ｆ的大小，只把力的方向变为水平去推这个静止的箱子，则箱子做匀加速直线运动，推力作用时间t1=4s后撤去，撤去后箱子做匀减速直线运动，加速度大小均为a=5m/s2,求箱子滑行的总位移为多大?
如图所示，半径为r=10cm、质量为M=1.8kg的均匀球靠竖直墙放置，左下方有一厚为h=4cm、质量为m=1kg的木块．（取g=10m/s2）
（1）若不计摩擦．用多大的水平力F推木块才能使球恰好离开地面？
（2）此时木块对地的压力？
试题篮
()
粤公网安备 44130202000953号
