高中物理相互作用、力与机械计算题

随着中国首艘航母“辽宁号”的下水，同学们对舰载机的起降产生了浓厚的兴趣. 从而编制了一道题目，请你阅读后求解.
（1）假设质量为的舰载机关闭发动机后在水平地面跑道上降落，触地瞬间的速度为，在跑道上滑行的图像见图.求舰载机滑行的最大距离和滑行时受到的阻力大小（忽略空气阻力）；
（2）为了让上述关闭发动机的舰载机在有限长度的航母甲板上降落停下来，甲板上设置了阻拦索让飞机减速.图为该舰载机勾住阻拦索后某一时刻的情景，此时加速度大小为（1）中的4倍，阻拦索夹角.舰载机所受甲板阻力与（1）中阻力相同，求此时阻拦索承受的拉力的大小.(忽略空气阻力，阻拦索认为水平)

一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线AB运动，如下图，AB与电场线夹角θ=30°，已知带电微粒的质量m=1.0×10^－7kg，电量q=1.0×10^－10C，A、B相距L=20cm。（取g=10m/s²，结果保留二位有效数字）求：

（1）电场强度的大小和方向？
（2）要使微粒从A点运动到B点，微粒射入电场时的最小速度是多少？

如图所示，A、B、C是半径R=5m的圆筒上一圆的三点，O为其圆心，AC垂直OB。在圆O平面加一场强E=2.5×10³V/m、水平向右、宽度与直径相同的匀强电场。现通过圆筒上唯一的小孔A沿AC直径射入速率为v的一带电粒子S，粒子质量m=2.5×10^-7kg、电量q=1.0×10^-7C，粒子S恰好能沿曲线直接运动到B点（不计粒子重力和粒子间的相互作用），求：

(1)粒子S的速率v为多大；
(2)若粒子S与筒壁的碰撞是弹性的（粒子S沿半径方向的分速度碰撞后反向、速度大小不变；垂直半径方向的分速度碰撞后不变），则粒子S在圆筒中运动的总时间是多少。

质量为m的小球A在光滑水平面上以速度v₀与质量为2m的静止小球B发生正碰后以v₀的速率反弹，试通过计算判断发生的是不是弹性碰撞．

水平导轨AB固定在支架CD上，其形状、尺寸如图所示。导轨与支架的总质量M=4kg，其重心在O点，它只能绕支架C点且垂直于纸面的水平轴转动。质量m=1kg的小铁块静止于水平导轨AB的A端，现受到水平拉力F=2.5N的作用。已知小铁块和导轨之间的动摩擦因数μ＝0.2。g取10m/s²，求：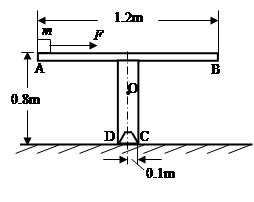

（1）小铁块刚开始运动时的加速度大小？
（2）小铁块运动到离A端多远时，支架将要开始翻转？
（3）若在小铁块运动的过程中，支架始终保持静止，则拉力F作用的最长时间为多少？

如图所示，杆OA长为R，可绕过O点的水平轴在竖直平面内转动，其端点A系   着一跨过定滑轮B、C的不可伸长的轻绳，绳的另一端系一物块M，滑轮的半径可忽略，B在O的正上方，OB之间的距离为H。某一时刻，当绳的BA段与OB之间的夹角为α＝30°时，杆的角速度为ω，求此时物块M的速率 v_M。

在双人花样滑冰比赛中，有时会看到被男运动员拉着的女运动员离开地面在空中做圆锥摆运动的精彩场面，质量为m的女运动员做圆锥摆运动时和水平冰面的夹角为θ，转动过程中女运动员的重心做匀速圆周运动的半径为r，重力加速度为g，求：
(1)该女运动员受到拉力的大小．
(2)该女运动员做圆锥摆运动的周期．

如图所示，ABC为一固定在竖直平面内的光滑轨道，BC段水平，AB段与BC段平滑连接.质量为m的小球从高为h处由静止开始沿轨道下滑，与静止在轨道BC段上质量为km的小球发生碰撞，碰撞前后两小球的运动方向处于同一水平线上。求：

（1）若两小球碰撞后粘连在一起，求碰后它们的共同速度；
（2）若两小球在碰撞过程中无机械能损失，为使两小球能发生第二次碰撞，求k应满足的条件。

如图所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点悬挂一个定滑轮(不计重力)，某人用它匀速地提起重物．已知重物的质量m＝30 kg，人的质量M＝50  kg，g取10 m/s².试求：
(1)此时地面对人的支持力的大小；
(2)轻杆BC和绳AB所受力的大小．

如图所示，用绳AC和BC吊起一个物体，绳AC与竖直方向的夹角为60°，绳BC与竖直方向的夹角为30°。若被吊起的物体重100N，试求绳AC和BC中张力分别为多大?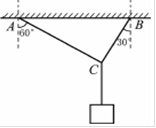

如图所示，用细绳将重球悬挂在光滑墙壁上，绳子与墙夹角为θ，球的重力为G。

（1）用力的分解法则作出重力和重力沿绳子方向及垂直墙壁方向的两个分力
（2）这两个分力的大小是多大？

如图所示，一只小球用绳OA和OB拉住，OA水平，OB与水平方向成60°角，这时OB绳受的拉力为8 N，求小球重力及OA绳拉力的大小．

一个质量为m、电量为+q的小球，用丝线悬挂在水平方向的匀强电场中，场强为E，平衡时悬线与竖直方向间夹角α="30" °(如图所示)，若将匀强电场E的方向逆时针转过角度β=45°，小球重新平衡时悬线与竖直方向间夹角正切为多大?（可以保留根号）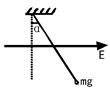

如图所示，倾斜轨道AB的倾角为37^o，CD、EF轨道水平，AB与CD通过光滑圆弧管道BC连接，CD右端与竖直光滑圆周轨道相连。小球可以从D进入该轨道，沿轨道内侧运动，从E滑出该轨道进入EF水平轨道。a、b为两完全相同的小球，a球由静止从A点释放，在C处与b球发生弹性碰撞。已知AB长为5R，CD长为R，重力加速度为g，小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5，sin37^o=0.6，cos37^o=0.8，圆弧管道BC入口B与出口C的高度差为1.8R。求：

⑴a球滑到斜面底端C时速度为多大？a、b球在C处碰后速度各为多少？
⑵要使小球在运动过程中不脱离轨道，竖直圆周轨道的半径R′应该满足什么条件？若R′=2.5R，两球最后所停位置距D（或E）多远？
注：在运算中，根号中的数值无需算出。

两人在河两岸用绳子拉小船使其在河流中行驶，甲的拉力是200 N，方向与航向间的夹角为60°，乙的拉力是200 N．要使小船能在河流中间沿直线行驶，那么乙用力的方向如何？小船受到两拉力的合力是多少？