如图所示,重为G的圆盘与一轻杆相连,杆与圆盘恰相切,支点为O。现用始终竖直向下的力F拉杆的另一端,使该端缓慢向下转动,则杆转到竖直之前,拉力F及其力矩M的变化情况是( )
| A.M变小,F不变. | B.M、F均变小. |
| C.M先变大再变小,F始终变大. | D.M、F均先变大再变小 |
一轻杆BO,其O端用光滑铰链铰于固定竖直杆AO上,B端挂一重物,且系一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图所示.现将细绳缓慢往左拉,使杆 BO与杆AO间的夹角θ逐渐减小,则在此过程中,拉力F及杆BO所受压力FN的大小变化情况是 ( )
| A.FN先减小,后增大 |
| B.FN始终不变 |
| C.F先减小,后增大 |
| D.F逐渐减小 |

如图所示,重为G的均匀棒,可绕上端O在竖直平面内转动。今在棒的下端用水平力F拉,使棒缓慢转动,直至转到水平方向为止,则拉力F和它的力矩M的变化情况: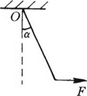
| A.都增大 | B.都减小 |
| C.F增大,M减小 | D.F减小,M增大 |
如图所示,AB为一轻质杠杆,O为支点,BO=2AO,AB两端分别悬挂实心铜球和实心铁球,杠杆在水平位置平衡,若将两球同时浸没在某液体中,液体的密度小于铜和铁的密度,则
| A.杠杆仍能保持平衡 | B.铜球一端下降 |
| C.铁球一端下降 | D.液体密度未知,故无法判断哪端下降 |
如图(1)所示,斜拉桥的塔柱两侧有许多钢索,它们的一端都系在塔柱上.对于每组对称钢索,它们的上端可以看成系在一起,即两根钢索对塔柱的拉力F1、F2作用在同一点.它们合起来对塔柱的作用效果应该让塔柱好像受到一个竖直向下的力F一样,如图(2)所示.这样,塔柱便能稳固地伫立在桥墩上,不会因钢索的牵拉而发生倾斜,甚至倒下.如果斜拉桥塔柱两侧的钢索不能呈对称分布如图(3)所示,要保持塔柱所受的合力竖直向下,那么钢索AC、AB的拉力FAC、FAB应满足
A. B.
B.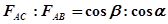
C. D.
D.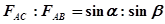
下列各图中,所有接触面都是光滑的,所有物体都处于静止状态.P、Q两个物体之间不存在弹力的是 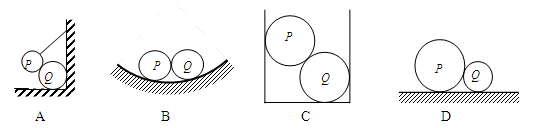
如图所示是杆秤的示意图,下列说法中正确的是
| A.秆秤是称量物体的重力的. |
| B.用提纽A时比用提纽B时的称量大. |
| C.只有秤杆是粗细均匀的,杆秤的刻度才是均匀的. |
| D.无论秤杆是否粗细均匀,杆秤的刻度都是均匀的. |
如图所示,两根重杆OA和OB,由铰链连接,并用铰链悬挂在天花板上,B位于O的正下方,若在B端分别施加图示方向的力F1、F2、F3和F4,则其中可能使两杆保持静止的是( )
| A.F1 | B.F2 |
| C.F3 | D.F4 |
如图2所示,棒AB的B端支在地上,另一端A受水平力F作用,棒平衡,则地面对棒B端作用力的方向为:( )
| A.总是偏向棒的左边,如F1 |
| B.总是偏向棒的右边,如F3 |
| C.总是沿棒的方向如F2 |
| D.总是垂直于地面向上如F4 |
如图所示, 型均匀杆总长为3L,AB水平,BC⊥AB,杆在竖直平面内可绕水平轴O转动,若在杆的右端A点加一方向竖直向下的力F,使AB顺时针缓慢转600过程中,以下说法正确的是( )
型均匀杆总长为3L,AB水平,BC⊥AB,杆在竖直平面内可绕水平轴O转动,若在杆的右端A点加一方向竖直向下的力F,使AB顺时针缓慢转600过程中,以下说法正确的是( )
| A.力F变大 |
| B.力F不变 |
| C.力F的力矩变小 |
| D.力F的力矩先变大后变小 |
如图所示,一根木棒在
点被悬挂起来,
,在
、
两点分别挂有两个和三个钩码,木棒处于平衡状态。如在木棒的
、
点各增加一个同样的钩码,则木棒()

| A. |
绕
|
| B. |
绕
|
| C. | 平衡可能被破坏,转动方向不定 |
| D. | 仍能保持平衡状态 |
如图1-54(原图1-57)所示的杆秤,O为提扭,A为刻度的起点,B为秤钩,P为秤砣,关于杆秤的性能,下述说法中正确的是( )。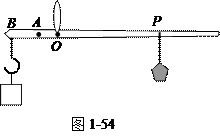
| A.不称物时,秤砣移至A处,杆秤平衡 |
| B.不称物时,秤砣移至B处,杆秤平衡 |
| C.称物时,OP的距离与被测物的质量成正比 |
| D.称物时,AP的距离与被测物的质量成正比 |
试题篮
()