高中物理力矩的平衡条件试题

如图丙所示，一质量分布均匀的梯子，重为G₁，斜搁在光滑的竖直墙上，重为G₂的人沿梯子从底端A开始匀速向上走，人的重心离地的高度h逐渐增大，整个过程梯子不滑动。如图丁所示为力F随高度h变化的函数图像，则下列关于力F的说法中正确的是：（　　）

A．F为墙面对梯子上端B施加的力

B．F为人对梯子施加的力

C．F为梯子对地面施加的弹力

D．F为梯子对地面施加的摩擦力

如图甲所示，滑轮质量、摩擦均不计，质量为2kg的物体在F作用下由静止开始向上做匀加速运动，其速度随时间的变化关系如图乙所示，由此可知（g取10m/s²）

A．物体加速度大小为2m/s^2

B．F的大小为21N

C．4s末F的功率大小为42W

D．4s内F做功的平均功率为42W

如图，倾角为，质量不计的支架的端有一大小与质量均可忽略的光滑定滑轮，点处有一固定转轴，⊥，＝＝0.3m。质量＝lkg的物体置于支架的端，并与跨过定滑轮的轻绳相连，绳另一端作用一竖直向下的拉力，物体在拉力作用下沿做匀速直线运动，己知物体与间的动摩擦因数＝0.3。为保证支架不绕点转动，物体向上滑行的最大距离＝m。若增大后，支架仍不绕点转动，物体能向上滑行的最大距离(填："大于"、"等于"或"小于"。)(取sin37°＝0.6，cos37°＝0.8)

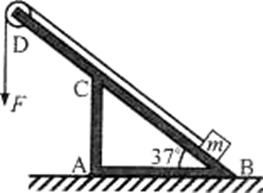
如图所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点悬挂一个定滑轮(不计重力)，某人用它匀速地提起重物．已知重物的质量m＝30 kg，人的质量M＝50  kg，g取10 m/s².试求：
(1)此时地面对人的支持力的大小；
(2)轻杆BC和绳AB所受力的大小．

如图所示，竖直放置的两平行带电金属板间的匀强电场中有一根质量为m的均匀绝缘杆，上端可绕轴O在竖直平面内转动，下端固定一个不计重力的点电荷A，带电量＋q。当板间电压为U₁时，杆静止在与竖直方向成＝45°的位置；若平行板以M、N为轴同时顺时针旋转＝15°的角，而仍要杆静止在原位置上，则板间电压应变为U₂。求：U₁/U₂的比值。

某同学是这样分析求解的：
两种情况中，都有力矩平衡的关系。设杆长为L，两板间距为d，当平行板旋转后，电场力就由变为，电场力对轴O的力臂也发生相应的改变，但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程，就可求解了。
你觉得他的分析是否正确？如果认为是正确的，请继续解答；如果认为有错误之处，请说明理由并进行解答。

如图所示，在光滑水平面上，一绝缘细杆长为，两端各固定着一个带电小球，处于水平方向、场强为E的匀强电场中，两小球带电量分别为＋q和－q，轻杆可绕中点O自由转动。在轻杆与电场线夹角为时，忽略两电荷间的相互作用，两电荷受到的电场力对O点的力矩大小为___________，两电荷具有的电势能为___________。

直杆AB和直角弯杆BCD按如图所示连接，A、B、D处均为铰链，杆及铰链的质量都不计。ABCD构成一长方形，将重力为G、可视为质点的物块放在图中P处。则

A．AB杆对BCD杆的作用力方向沿BC连线向下
B．BCD杆对AB杆的作用力方向沿DB连线斜向上
C．若AP间距变大，BCD杆对AB杆的作用力变大
D．若AP间距变大，AB杆对BCD杆的作用力对转动轴D的力矩不变

如图，一质量为M的质量分布不均匀的多边形板AOB，边OA⊥OB且OA＝OB＝L，O点为水平固定转动轴，现用一水平拉力拉住A点，维持三角板处于OA竖直的静止状态，拉力大小为F，重力加速度为g，则三角板重心到AO的距离为（     ）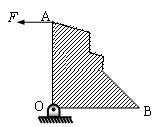

A．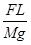

B．

C．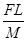

D．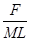

如图所示，质量为m、边长为l的等边三角形ABC导线框，在A处用轻质细线竖直悬挂于质量也为m、长度为L的水平均匀硬杆一端，硬杆另一端通过轻质弹簧连接地面，离杆左端L/3处有一光滑固定转轴O。垂直于ABC平面有一个水平方向的匀强磁场，磁感应强度大小为B，当在导线框中通以逆时针方向大小为I的电流时，AB边受到的安培力大小为________，此时弹簧对硬杆的拉力大小为________。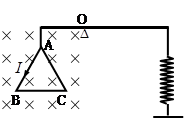

如图所示，AB棒与BC棒用光滑的饺链铰在B点，A、C也用光滑的饺链铰于墙上．BC棒水平，AB棒与竖直成45°角，两棒等长等重．则两捧在B点的相互作用力的方向：

(A)可能与AB棒平行.               (B)可能与BC棒平行.   
(C)可能与虚线DE平行.    (D)可能与虚线FG平行.

如图为悬挂街灯的支架示意图，横梁BE质量为6kg，重心在其中点。直角杆A.DC重力不计，两端用铰链连接。已知BE=3m，BC=2m，∠A.CB=30°，横梁E处悬挂灯的质量为2kg，则直角杆对横梁的力矩为_______N·m，直角杆对横梁的作用力大小为_______N。（重力加速度g=l0m/s²）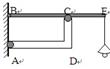

如图所示，竖直放置的两平行带电金属板间的匀强电场中有一根质量为m的均匀绝缘杆，上端可绕轴O在竖直平面内转动，下端固定一个不计重力的点电荷A，带电量＋q。当板间电压为U₁时，杆静止在与竖直方向成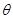＝45°的位置；若平行板以M、N为轴同时顺时针旋转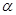＝15°的角，而仍要杆静止在原位置上，则板间电压应变为U₂。求：U₁/U₂的比值。

某同学是这样分析求解的：
两种情况中，都有力矩平衡的关系。设杆长为L，两板间距为d，当平行板旋转后，电场力就由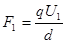变为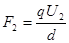，电场力对轴O的力臂也发生相应的改变，但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程，就可求解了。
你觉得他的分析是否正确？如果认为是正确的，请继续解答；如果认为有错误之处，请说明理由并进行解答。

如图所示，一根木棒AB在O点被悬挂起来，AO＝OC，在A、C两点分别挂有两个和三个钩码，木棒处于平衡状态。如在木棒的A、C点各增加一个同样的钩码，则木棒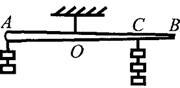

A．绕O点顺时针方向转动

B．绕O点逆时针方向转动

C．平衡可能被破坏，转动方向不定

D．仍能保持平衡状态

塔式起重机的结构如图所示，设机架重P＝400 kN，悬臂长度为L＝10 m，平衡块重W＝200 kN，平衡块与中心线OO^/的距离可在1 m到6 m间变化，轨道A、B间的距离为4 m。

⑴当平衡块离中心线1 m，右侧轨道对轮子的作用力f_B是左侧轨道对轮子作用力f_A的2倍，问机架重心离中心线的距离是多少？
⑵当起重机挂钩在离中心线OO^/10 m处吊起重为G＝100 kN的重物时，平衡块离OO^/的距离为6 m，问此时轨道B对轮子的作用力F_B时多少？

图中是用电动砂轮打磨工件的装置，砂轮的转轴过图中O点垂直于纸面，AB是一长度，质量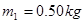的均匀刚性细杆，可绕过A端的固定轴在竖直面（图中纸面）内无摩擦地转动，工件C固定在AB杆上，其质量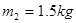，工件的重心、工件与砂轮的接触点P以及O点都在过AB中点的竖直线上，P到AB杆的垂直距离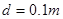，AB杆始终处于水平位置，砂轮与工件之间的动摩擦因数

（1）当砂轮静止时，要使工件对砂轮的压力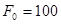N，则施于B端竖直向下的力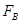应是多大？
（2）当砂轮逆时针转动时，要使工件对砂轮的压力仍为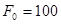N，则施于B端竖直向下的力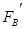应是多大？