高中物理平抛运动计算题

在竖直平面内固定一轨道ABCO，AB段水平放置，长为4m，BCO段弯曲且光滑，轨道在D点的曲率半径为1.5m; -质量为1.0 kg、可视作质点的圆环套在轨道上，圆环与轨道AB段间的动摩擦因数为0.5.建立如图所示的直角坐标系，圆环在沿x轴正方向的恒力F作用下，从A(-7m,2m)点由静止开始运动，到达原点D时撤去恒力F，水平飞出后经过D (6m，3m)点。重力加速度g取lOm/s2，不计空气阻力，求：

(1)圆环到达D点时对轨道的压力；
(2)恒力F的大小；
(3)圆环在AB段运动的时间．

如图所示，在竖直平面的xoy坐标系内，一根长为l的不可伸长的细绳，一端固定在拉力传感器A上，另一端系一质量为m的小球．x轴上的P点固定一个表面光滑的小钉，P点与传感器A相距．现拉小球使细绳绷直并处在水平位置，然后由静止释放小球，当细绳碰到钉子后，小球可以绕钉子在竖直平面内做圆周运动．已知重力加速度大小为g，求：

(1)若小球经过最低点时拉力传感器的示数为7mg，求此时小球的速度大小；
(2)传感器A与坐标原点O之间的距离；
(3)若小球经过最低点时绳子恰好断开，请确定小球经过y轴的位置．

如图所示，在冬奥会上，跳台滑雪运动员从滑道上的A点由静止滑下，经时间t₀从跳台末端的O点沿水平方向飞出。O点又是斜坡OB的起点，A点与O点在竖直方向的高度差为h，斜坡OB的倾角为θ。运动员的质量为m，重力加速度为g。不计一切摩擦和空气阻力。求：

⑴从A点到O点的运动过程中，重力对运动员做功的平均功率；
⑵运动员在斜坡OB上的落点到O点的距离S；
⑶若运动员在空中飞行时处理好滑雪板和水平面的夹角，便可获得一定的竖直向上的升力。假设该升力为运动员全重的5﹪，求实际落点到O点的距离将比第⑵问求得的距离远百分之几？（保留三位有效数字）

分如图所示，光滑圆弧轨道最低点与光滑斜面在B点用一段光滑小圆弧平滑连接，可认为没有能量的损失，圆弧半径为R=0.5m，斜面的倾角为45⁰，现有一个可视为质点、质量为m=0.1kg的小球从斜面上A点由静止释放，通过圆弧轨道最低点B时对轨道的压力为6N．以B点为坐标原点建立坐标系如图所示(g=l0m/s²)求：

（1）小球最初自由释放位置A离最低点B的高度h.
（2）小球运动到C点时对轨道的压力的大小；
（3）小球从离开C点至第一次落回到斜面上，落点的坐标是多少?

如图所示为浦江中学物理课外兴趣小组在某次四驱车比赛时轨道的一小段。小虎同学控制的四驱车（可视为质点），质量m=1.0kg，额定功率为P=9W，四驱车到达水平平台上A点时速度很小（可视为0），此时启动四驱车的发动机并以额定功率运动，当四驱车到达平台边缘B点时恰好达到最大速度，并从B点水平飞出，恰能从C点沿切线方向飞入粗糙的竖直圆形轨道内侧，到达C点时的速度大小为5m/s，且∠α=53°，四驱车沿CDE运动到最高点F时轨道对它的压力恰为零，已知AB间的距离L=6m，圆弧轨道半径Ｒ＝0.4m，重力加速度g取10m/s²，不计空气阻力。sin53°=0.8，cos53°=0.6，求：

（1）四驱车运动到B点时的速度大小；
（2）发动机在水平平台上工作的时间；
（3）四驱车在圆轨道上从C点运动到F点的过程中克服阻力做的功。

如图所示，半径R＝0.4 m的光滑圆弧轨道BC固定在竖直平面内，轨道的上端点B和圆心O的连线与水平方向的夹角θ＝30°，下端点C为轨道的最低点且与粗糙水平面相切，一根轻质弹簧的右端固定在竖直挡板上。质量m＝0.1 kg的小物块（可视为质点）从空中A点以v₀＝2 m/s的速度被水平抛出，恰好从B点沿轨道切线方向进入轨道，经过C点后沿水平面向右运动至D点时，弹簧被压缩至最短，C、D两点间的水平距离L＝1.2m，小物块与水平面间的动摩擦因数μ＝0.5，g取10 m/s²。求：

（1）小物块经过圆弧轨道上B点时速度v_B的大小；
（2）小物块经过圆弧轨道上C点时对轨道的压力大小；
（3）弹簧的弹性势能的最大值E_pm。

如图所示，直角坐标系xOy位于竖直平面内，x轴与绝缘的水平面重合，在y轴右方有垂直纸面向里的匀强磁场和竖直向上的匀强电场．质量为m₂＝8×10^－3 kg的不带电小物块静止在原点O，A点距O点l＝0.045 m，质量m₁＝1×10^－3 kg的带电小物块以初速度v₀＝0.5 m/s从A点水平向右运动，在O点与m₂发生正碰并把部分电量转移到m₂上，碰撞后m₂的速度为0.1 m/s，此后不再考虑m₁、m₂间的库仑力。已知电场强度E＝40 N/C，小物块m₁与水平面的动摩擦因数为μ＝0.1，取g＝10 m/s²，求：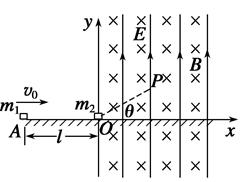

(1)碰后m₁的速度；
(2)若碰后m₂做匀速圆周运动且恰好通过P点，OP与x轴的夹角θ＝30°，OP长为l_OP＝0.4 m，求磁感应强度B的大小；
(3)其他条件不变，若改变磁场磁感应强度B′的大小，使m₂能与m₁再次相碰，求B′的大小。

(19分)如图所示，足够长的光滑绝缘水平台左端固定一被压缩的绝缘轻质弹簧，一个质量、电量的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度，倾斜轨道与水平方向夹角为、倾斜轨道长为，带电小球与倾斜轨道的动摩擦因数。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强。（cos37°=0.8，sin37°=0.6，取g=10m/s²）求：

（1）被释放前弹簧的弹性势能？
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径应该满足什么条件？
（3）如果竖直圆弧轨道的半径，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？

某游戏装置放在竖直平面内，如图所示，装置由粗糙抛物线形轨道AB和光滑的圆弧轨道BCD构成，控制弹射器可将穿在轨道上的小球以不同的水平初速度由A点射入，最后小球将由圆轨道的最高点D水平抛出，落入卡槽中得分，圆弧半径为R，O′为圆弧的圆心，C为圆弧轨道最低点，抛物线轨道上A点在坐标轴的原点O上，轨道与圆弧相切于B点，抛物线轨道方程为y=ax²（0＜a＜），∠BO′C=θ，x轴恰好将半径O′D分成相等的两半，交点为P，x轴与圆弧交于Q点，则：   

（1）将小球以某一初速度水平由A点射入轨道，小球沿轨道运动到与A等高处Q，速度减为0，试求小球运动到B点的速度；
（2）由（1）得到的B点的速度，能否求出小球在A点射入的速度，如果能请求出v₀，不能，请说明理由（3）试求在多次弹射小球的过程中，机械能损失最小的一次，小球在最高点D对轨道的作用力与最低点C对轨道的作用力的比值．

如图所示，一质量为m=0.5kg，电荷量为q=+0.2C的小物块（可视为质点），放在离地面高度为h=5m的水平放置、厚度不计的绝缘圆盘边缘，并随圆盘一起绕中心转轴顺时针做匀速圆周运动，圆盘的角速度为ω=2rad/s，半径为r=1m，圆盘和小物块之间的动摩擦因数为μ=0.5。以圆盘左侧垂直于纸面的切面和过圆盘圆心O点与空间中A点的竖直平面为界（两平面平行），将空间分为Ⅰ、Ⅱ、Ⅲ三个空间区域，当小物块转动时，Ⅰ区域出现随时间均匀增大的电场E（图中未画出），电场方向是竖直方向。当E增大到E₁时，小物块刚好从空间中的A点离开圆盘，且垂直于Ⅰ、Ⅱ区域边界进入Ⅱ区域，此时，Ⅱ区域和Ⅲ区域立即出现一竖直向上的匀强电场E₂（图中未画出），E₂=25N/C，且Ⅲ区域有一垂直于纸面向里的匀强磁场，磁场宽度为L=4m，g=10m/s²。求：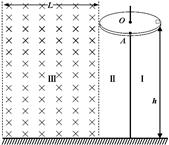

（1）E₁的大小和方向；
（2）若小物块在磁场宽度范围内落地，则磁感应强度B的取值范围是多少？
（3）现将磁感应强度B取某一值，当小物块离开A后一小段时间，紧贴圆盘圆心O点下方以速度v₀=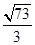m/s水平抛出一木制小球，最终两者在磁场宽度范围内的地面上相遇，则从小物块离开A点时开始计时，抛出木制小球的时刻t为多少？

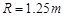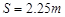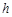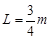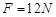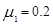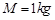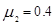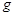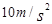如图所示，四分之一圆轨道OA与传送带相切相连，下方的CD水平轨道与他们在同一竖直面内。圆轨道OA的半径，传送带长，圆轨道OA光滑，AB与CD间的高度差为。一滑块从O点静止释放，当滑块经过B点时（无论传送带是否运动），静止在CD上的长为的木板（此时木板的末端在B点的正下方）在的水平恒力作用下启动，此时滑块落入木板中，已知滑块与传送带的摩擦因数，木板的质量，木板与CD间的摩擦因数为，取，求：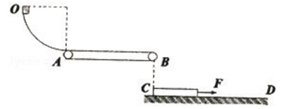

（1）如果传送带静止，求滑块到达B点的速度。
（2）如果传送带静止，求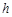的取值范围。
（3）如果传送带可以以任意速度传动，取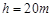，试判断滑块还能否落在木板上。

如图，在粗糙水平台阶上静止放置一质量m=0.5kg的小物块，它与水平台阶表面的动摩擦因数μ=0.5，且与台阶边缘O点的距离s=5m．在台阶右侧固定了一个圆弧挡板，圆弧半径R=1m，圆弧的圆心也在O点．今以O点为原点建立平面直角坐标系．现用F=5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板．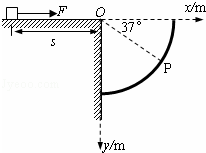

（1）若小物块恰能击中挡板上的P点（OP与水平方向夹角为37°），求其离开O点时的速度大小；
（2）为使小物块击中挡板，求拉力F作用的最短时间；
（3）改变拉力F的作用时间，使小物块击中挡板的不同位置，求击中挡板时小物块动能的最小值．

某人站在高60 m的平台边缘，以20 m/s的初速度竖直向上抛出一石块，不考虑空气阻力，取g="10" m/s²求：
（1）石块上升的最大高度。
（2）石块从抛出到落地的时间。
（3）石块落到地面时的速度。

如图所示，已知塔高H＝45m，在与塔底部水平距离为x处有一电子抛靶装置，圆形靶可被竖直向上抛出，初速度为υ₁，且大小可以调节．当该人看见靶被抛出时立即射击，子弹以υ₂＝100m/s的速度水平飞出．不计人的反应时间及子弹在枪膛中的运动时间，且忽略空气阻力及靶的大小（g取10 m/s²）。

（1）若x＝200m，υ₁＝20m/s时，试通过计算说明靶能否被击中？
（2）当x的取值在什么范围时，无论υ₁多大，靶都不能被击中？

某校物理兴趣小组决定举行遥控赛车比赛，比赛路径如图所示。可视为质点的赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直半圆轨道，并通过半圆轨道的最高点C，才算完成比赛。B是半圆轨道的最低点，水平直线轨道和半圆轨道相切于B点。已知赛车质量m=0．5kg，通电后以额定功率P=2W工作，进入竖直圆轨道前受到的阻力恒为F_f=0．4N，随后在运动中受到的阻力均可不计，L=10．00m，R=0．32m，(g取10m/s²)。求：

（1）要使赛车完成比赛，赛车在半圆轨道的B点对轨道的压力至少多大；
（2）要使赛车完成比赛，电动机至少工作多长时间；
（3）若电动机工作时间为 t₀=5s，当R为多少时赛车既能完成比赛且飞出的水平距离又最大，水平距离最大是多少。