高中物理平抛运动试题

如图所示，直角坐标系xOy位于竖直平面内，x轴与绝缘的水平面重合，在y轴右方有垂直纸面向里的匀强磁场和竖直向上的匀强电场．质量为m₂＝8×10^－3 kg的不带电小物块静止在原点O，A点距O点l＝0.045 m，质量m₁＝1×10^－3 kg的带电小物块以初速度v₀＝0.5 m/s从A点水平向右运动，在O点与m₂发生正碰并把部分电量转移到m₂上，碰撞后m₂的速度为0.1 m/s，此后不再考虑m₁、m₂间的库仑力。已知电场强度E＝40 N/C，小物块m₁与水平面的动摩擦因数为μ＝0.1，取g＝10 m/s²，求：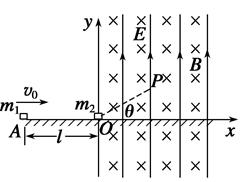

(1)碰后m₁的速度；
(2)若碰后m₂做匀速圆周运动且恰好通过P点，OP与x轴的夹角θ＝30°，OP长为l_OP＝0.4 m，求磁感应强度B的大小；
(3)其他条件不变，若改变磁场磁感应强度B′的大小，使m₂能与m₁再次相碰，求B′的大小。

如图所示为浦江中学物理课外兴趣小组在某次四驱车比赛时轨道的一小段。小虎同学控制的四驱车（可视为质点），质量m=1.0kg，额定功率为P=9W，四驱车到达水平平台上A点时速度很小（可视为0），此时启动四驱车的发动机并以额定功率运动，当四驱车到达平台边缘B点时恰好达到最大速度，并从B点水平飞出，恰能从C点沿切线方向飞入粗糙的竖直圆形轨道内侧，到达C点时的速度大小为5m/s，且∠α=53°，四驱车沿CDE运动到最高点F时轨道对它的压力恰为零，已知AB间的距离L=6m，圆弧轨道半径Ｒ＝0.4m，重力加速度g取10m/s²，不计空气阻力。sin53°=0.8，cos53°=0.6，求：

（1）四驱车运动到B点时的速度大小；
（2）发动机在水平平台上工作的时间；
（3）四驱车在圆轨道上从C点运动到F点的过程中克服阻力做的功。

如图所示，质量为m＝0.2kg的小球（可视为质点）从水平桌面右端点A以初速度v₀水平抛出，桌面右侧有一竖直放置的光滑轨道MNP，其为半径R＝0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径.P点到桌面的竖直距离为R.小球飞离桌面后恰由P点无碰撞地落入圆轨道，取g＝10 m/s².

（1）求小球在A点的初速度v₀及AP间的水平距离x;
（2）求小球到达圆轨道最低点N时对N点的压力;
（3）判断小球能否到达圆轨道最高点M.

“要打战必打胜战”，我人民海军为此进行登陆演练，假设一艘战舰因吨位大吃水太深，只能停锚在离海岸登陆点x＝1 km处．登陆队员需要从较高的军舰甲板上，利用绳索下滑到登陆快艇上再行登陆接近目标，若绳索两端固定好后，与竖直方向的夹角θ＝37°，为保证行动最快，队员甲先匀加速滑到某最大速度，再靠摩擦匀减速滑至快艇，速度刚好为零，在队员甲开始下滑时，队员乙在甲板上同时开始向快艇以速度平抛救生圈，第一个刚落到快艇，接着抛第二个，结果第二个救生圈刚好与甲队员同时抵达快艇（快艇可视为质点），若人的质量m，重力加速度g＝10 m/s²，问：

（1）军舰甲板到快艇的竖直高度H为多少？
队员甲在绳索上运动的时间t₀为多少？
（2）若加速过程与减速过程中的加速度大小相等，则队员甲在何处速度最大？最大速度多大？
（3）若登陆艇额定功率5 kW，载人后连同装备总质量为10³ kg，从静止开始以最大功率向登陆点加速靠近，到达岸边时刚好能达到最大速度10 m/s，若登陆舰前进时阻力恒定，则登陆艇运动的时间t′为多少？

如图所示，斜面与水平面夹角，在斜面上空A点水平抛出两个小球小球a、b，初速度分别为v_a、v_b，a球恰好垂直打到斜面上M点，而b球落在斜面上的N点，而AN恰好垂直于斜面，则（   ）

A．a、b两球水平位移之比

B．a、b两球水平位移之比

C．a、b两球下落的高度过之比

D．a、b两球下落的高度过之比

如图所示，小球从A点以固定的初速度v₀水平抛出，空气阻力不计，A点右下方有一带挡板的轮子，轮子与小球运动轨迹在同一竖直面内。轮子的半径为R，抛出点A比轮轴高h，挡板的初位置在与轮轴等高的B点，调整轮轴O的位置，使平抛轨迹与轮缘相切于C，OC与OB间夹角为θ角。求：

(l)小球抛出的初速度v₀大小为多少；
(2)小球抛出的瞬间轮子开始顺时针匀速转动，若不计挡板大小，要使小球打在挡板上，轮子转动的角速度为多少？

滑板运动是极限运动的鼻祖，许多极限运动项目均由滑板项目延伸而来。如图所示是滑板运动的轨道，BC和DE是两段光滑圆弧形轨道，BC段的圆心为O点，圆心角为60º，半径OC与水平轨道CD垂直，水平轨道CD段粗糙且长8m。一运动员从轨道上的A点以3m/s的速度水平滑出，在B点刚好沿轨道的切线方向滑入圆弧轨道BC，经CD轨道后冲上DE轨道，到达E点时速度减为零，然后返回。已知运动员和滑板的总质量为60kg，B、E两点与水平面CD的竖直高度分别为h和H，且h=2m，H=2.8m，取10m/s²。求：

（1）运动员从A运动到达B点时的速度大小v_B；
（2）轨道CD段的动摩擦因数；
（3）通过计算说明，第一次返回时，运动员能否回到B点？如能，请求出回到B点时速度的大小；如不能，则最后停在何处？

如图，BC为半径等于Ｒ＝竖直放置的光滑细圆管，O为细圆管的圆心，BO与竖直线的夹角为45°；在圆管的末端C连接一光滑水平面，水平面上一质量为Ｍ＝1.5kg的木块与一轻质弹簧拴接，轻弹簧的另一端固定于竖直墙壁上．现有一质量为m=0.5kg的小球从Ｏ点正上方某处Ａ点以v₀水平抛出，恰好能垂直OB从B点进入细圆管，小球从进入圆管开始即受到始终竖直向上的力F=5N的作用，当小球运动到圆管的末端C时作用力F立即消失．小球过后与木块发生完全非弹性碰撞（g=10m/s²）．求：

（1）小球在Ａ点水平抛出的初速度v₀；
（2）在圆管运动中圆管对小球的支持力Ｎ；
（3）弹簧的最大弹性势能Ｅ_Ｐ．

如图所示，一质量为M＝5.0kg，长度L=4m的平板车静止在水平地面上，距离平板车右侧S=16.5m处有一固定障碍物．障碍物上固定有一电动机A。另一质量为m＝2.0kg可视为质点的滑块，以v₀＝8m/s的水平初速度从左端滑上平板车，同时电动机A对平板车施加一水平向右、大小为22.5N的恒力F．1s后电动机A突然将功率变为P=52.5w并保持不变，直到平板车碰到障碍物停止运动时，电动机A也同时关闭。滑块沿水平飞离平板车后，恰能无碰撞地沿圆弧切线从B点滑入光滑竖直圆弧轨道，并沿轨道下滑．已知平板车间与滑块的动摩擦因数μ₁＝0.5，平板车与地面的动摩擦因数μ₂＝0.25，圆弧半径为R＝1.0m，圆弧所对的圆心角∠BOD＝θ＝106⁰，g取10m/s²，sin53°＝0.8，cos53°＝0.6，不计空气阻力，求：

（1）0 1s时间内，滑块相对小车运动的位移x；
（2）电动机A做功W；
（3）滑块运动到圆弧轨道最低点C时对轨道压力的大小F_N．

如图所示，半径R=0.6m的光滑圆弧轨道BCD与足够长的粗糙轨道DE在D处平滑连接，O为圆弧轨道BCD的圆心，C点为圆弧轨道的最低点，半径OB、OD与OC的夹角分别为53°和37°。将一个质量m=0.5kg的物体(视为质点)从B点左侧高为h=0.8m处的A点水平抛出，恰从B点沿切线方向进入圆弧轨道。已知物体与轨道DE间的动摩擦因数=0.8，重力加速度g取10m/s²，sin37°="0." 6，cos37°=0.8。求：

（1）物体水平抛出时的初速度大小v₀；
（2）物体在轨道DE上运动的路程s。

滑雪者从A点由静止沿斜面滑下，经一平台水平飞离B点，地面上紧靠着平台有一个水平台阶，空间几何尺度如图所示、斜面、平台与滑雪板之间的动摩擦因数为m，假设滑雪者由斜面底端进入平台前后速度大小不变。求：

(1)滑雪者离开B点时的速度大小；
(2)滑雪者从B点开始做平抛运动的水平距离s。

宇航员站在一星球表面上的h高处,沿水平方向抛出一个小球,经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L;若抛出时的初速度增大两倍,则抛出点与落地点之间的距离变为L . 已知两落地点在同一水平面上.求该星球表面的重力加速度. 

如图，位于竖直水平面内的光滑轨道由四分之一圆弧ab和抛物线bc组成，圆弧半径Oa水平，b点为抛物线顶点。已知h=2m，，s=，取重力加速度大小。

（1）一小环套在轨道上从a点由静止滑下，当其在bc段轨道运动时，与轨道之间无相互作用力，求圆弧轨道的半径；
（2）若环从b点由静止因微小扰动而开始滑下，求环到达c点时速度的水平分量的大小。

高一某班某同学为了更精确的描绘出物体做平抛运动的轨迹，使用闪光照相拍摄小球在空中的位置，如图所示为一小球做平抛运动的闪光照相照片的一部分，图中背景方格的边长表示实际长度8mm，如果取g＝10m/s²，那么：

（1）照相机的闪光周期是　　　s；
（2）小球运动中水平分速度的大小是　　　　m/s；
（3）小球经过B点时的速度大小是　　　　m/s。

如图所示，在足够长的斜面上A点，以水平速度v₀抛出一个小球，不计空气阻力，它落捌斜面上所用的时间为t₁；若将此球改用2v₀水平速度抛出，它落到斜面上所用时间为t₂，则t₁：t₂为

A．1：l

B．1：2

C．1：3

D．1：4