两颗靠得较近的天体容易形成双星系统.它们在万有引力的作用下,绕其连线上的某一点做周期相同的匀速圆周运动.由天文观测所得,某双星系统中,两星体中心距离为r,两星体的质量分别为m1和m2.则两星体绕共同圆心做匀速圆周运动的轨道半径之比r1∶r2=___________,它们共同的角速度为____________.(引力常量为G)
土星周围有美丽壮观的“光环”,组成环的颗粒是大小不等、线度从1 μm到10 m的岩石、尘埃,类似于卫星,它们与土星中心的距离从7.3×104 km延伸到1.4×105 km.已知环的外缘颗粒绕土星做圆周运动的周期约为14 h,引力常量为6.67×10-11 N·m2/kg2,则土星的质量约为(估算时不考虑环中颗粒间的相互作用)( )
| A.9.0×1016 kg | B.6.4×1017 kg |
| C.9.0×1025 kg | D.6.4×1026 kg |
由“嫦娥奔月”到“万户飞天”,由“东方红”乐曲响彻寰宇到航天员杨利伟、费俊龙、聂海胜遨游太空,中华民族的航天梦想已变成现实.“神舟”六号飞船升空后,先运行在近地点高度200 km、远地点高度350 km的椭圆轨道上,实施变轨后进入343 km的圆轨道,设变轨后做匀速圆周运动,共运行n周,起始时刻为t1,结束时刻为t2,运行速度为v,半径为r.则计算其运行周期可用( )
A.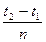 |
B. |
C.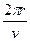 |
D.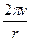 |
如图中的圆a、b、c,其圆心均在地球的自转轴线上,对卫星环绕地球做匀速圆周运动而言( )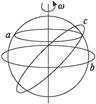
| A.卫星的轨道只可能为a |
| B.卫星的轨道可能为b |
| C.卫星的轨道可能为c |
| D.同步卫星的轨道一定为b |
组成星球的物质是靠引力吸引在一起的,这样的星球有一个最大的自转速率,如果超过了该速率,星球的万有引力将不足以维持其赤道附近的物体做匀速圆周运动.由此可以得到半径为R、密度为ρ、质量为M且均匀分布的星球的最小自转周期T.运载赤道则下列表达式中正确的是( )
A.T=2π |
B.T=2π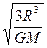 |
C.T= 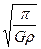 |
D.T= |
如图所示,在圆轨道上运行的国际空间站里,一宇航员A静止(相对空间舱)“站”在舱内朝向地球一侧的“地面”B上.则下列说法正确的是( )
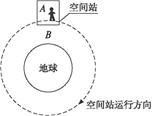
| A.宇航员A不受重力作用 |
| B.宇航员A所受重力与他在该位置所受的万有引力相等 |
| C.宇航员A与“地面”B之间无弹力作用 |
| D.若宇航员A将手中一小球无初速(相对空间舱)释放,该小球将落到“地面”B上 |
最近,科学家在望远镜中看到太阳系外某一恒星有一行星,并测得它围绕该恒星运行一周所用的时间为1 200年,它与该恒星的距离为地球到太阳距离的100倍.假定该行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周,仅利用以上两个数据可以求出的量有( )
| A.恒星质量与太阳质量之比 |
| B.恒星密度与太阳密度之比 |
| C.行星质量与地球质量之比 |
| D.行星运行速度与地球公转速度之比 |
设行星绕恒星的运动轨道是圆,则其运行周期T的平方与其运动轨道半径R的三次方之比为常数,即R3/T2=k,那么k的大小( )
| A.只与行星质量有关 |
| B.只与恒星质量有关 |
| C.与恒星及行星的质量均有关 |
| D.与恒星的质量及行星的速率有关 |
已知物体从地球上的逃逸速度(第二宇宙速度)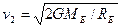 ,其中G、ME、RE分别是引力常量、地球的质量和半径。已知G=6.7×10-11N·m2/kg2,c=3.0×108m/s,求下列问题:(1)逃逸速度大于真空中光速的天体叫做黑洞,设某黑洞的质量等于太阳的质量M=2.0×1030kg,求它的可能最大半径(这个半径叫Schwarhid半径);(2)在目前天文观测范围内,物质的平均密度为10-27kg/m3,如果认为我们的宇宙是这样一个均匀大球体,其密度使得它的逃逸速度大于光在真空中的速度c,因此任何物体都不能脱离宇宙,问宇宙的半径至少多大?(最后结果保留两位有效数字)
,其中G、ME、RE分别是引力常量、地球的质量和半径。已知G=6.7×10-11N·m2/kg2,c=3.0×108m/s,求下列问题:(1)逃逸速度大于真空中光速的天体叫做黑洞,设某黑洞的质量等于太阳的质量M=2.0×1030kg,求它的可能最大半径(这个半径叫Schwarhid半径);(2)在目前天文观测范围内,物质的平均密度为10-27kg/m3,如果认为我们的宇宙是这样一个均匀大球体,其密度使得它的逃逸速度大于光在真空中的速度c,因此任何物体都不能脱离宇宙,问宇宙的半径至少多大?(最后结果保留两位有效数字)
试题篮
()