两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R,其运动周期为T,求两星的总质量。
中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T= s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67
s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67 10
10 m
m /kg·s
/kg·s )
)
宇航员在一星球表面上的某高处,沿水平方向抛出一小球。经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时初速度增大到2倍,则抛出点与落地点之间的距离为 L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
如图所示,在距一质量为M、半径为R、密度均匀的球体中心2R处,有一质量为m的质点,M对m的万有引力的大小为F。现从M中挖出一半径为r的球体,如图,OO′=R/2。求M中剩下的部分对m的万有引力的大小。
在天文学中,把两颗相距较近的恒星叫双星,已知两恒星的质量分别为m和M,两星之间的距离为L,两恒星分别围绕共同的圆心作匀速圆周运动,如图所示,求恒星运动的半径和周期。
如图所示,内半径为R的光滑圆轨道竖直放置,长度比2R稍小的轻质杆两端各固定一个可视为质点的小球A和B,把轻杆水平放入圆形轨道内,若mA=2m、mB=m,重力加速度为g,现由静止释放两球使其沿圆轨道内壁滑动,当轻杆到达竖直位置时,求:
A、B两球的速度大小;
A球对轨道的压力;
某球形天体的密度为ρ0,引力常量为G.证明对环绕密度相同的球形天体表面运行的卫星,运动周期与天体的大小无关.(球的体积公式为
 ,其中R为球半径)
,其中R为球半径)若球形天体的半径为R,自转的角速度为
 ,表面周围空间充满厚度
,表面周围空间充满厚度 (小于同步卫星距天体表面的高度)、密度ρ=
(小于同步卫星距天体表面的高度)、密度ρ= 的均匀介质,试求同步卫星距天体表面的高度.
的均匀介质,试求同步卫星距天体表面的高度.
已知地球与月球质量比为8:1,半径之比为3.8:1,在地球表面上发射卫星,至少需要7.9km/s的速度,求在月球上发现一颗环绕月球表面运行的飞行物需要多大的速度?
阅读下列材料,并结合材料解题
开普勒从1909年——1919年发表了著名的开普勒行星三定律:
第一定律:所有的行星分别在大小不同的椭圆轨道上绕太阳运动,太阳在这个椭圆的一个焦点上
第二定律:太阳和行星的连线在相等的时间内扫过相等的面积
第三定律:所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等
实践证明,开普勒三定律也适用于人造地球卫星的运动,如果人造地球卫星沿半径为r的圆形轨道绕地球运动,当开动制动发动机后,卫量速度降低并转移到与地球相切的椭圆轨道,如图问在这之后,卫星经过多长时间着陆?空气阻力不计,地球半径为R,地球表面重力加速度为g,圆形轨道作为椭圆轨道的一种特殊形式。
地核体积约为地球体积的16%,地球质量约为地球质量的34%,引力常量取G=6.7×10-11Nm2/kg2,地球半径取R=6.4×106m,地球表面重力加速度取g=9.8m/s2,试估算地核的平均密度(结果取2位有效数字)。
开普勒三定律也适用于神舟七号飞船的变轨运动. 飞船与火箭分离后进入预定轨道, 飞船在近地点(可认为近地面)开动发动机加速, 之后,飞船速度增大并转移到与地球表面相切的椭圆轨道, 飞船在远地点再次点火加速, 飞船沿半径为r的圆轨道绕地运动. 设地球半径为R,地球表面的重力加速度为g,若不计空气阻力,试求神舟七号从近地点到远地点时间(变轨时间).
神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它星体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图18所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.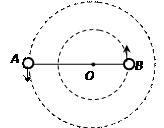
可见星A所受暗星B的引力FA可等效为位于O点处质量为
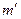 的星体(可视为质点)对它的引力,设A和B的质量分别为m1、m2,试求
的星体(可视为质点)对它的引力,设A和B的质量分别为m1、m2,试求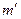 (用m1、m2表示);
(用m1、m2表示);求暗星B的的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式;
恒星演化到末期,如果其质量大于太阳质量ms的2倍,它将有可能成为黑洞.若可见星A的速率
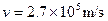 ,运行周期
,运行周期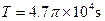 ,质量m1=6ms,试通过估算来判断暗星B有可能是黑洞吗? 图18
,质量m1=6ms,试通过估算来判断暗星B有可能是黑洞吗? 图18
( ,
,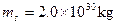 )
)
试题篮
()