地球质量为M,半径为R,万有引力恒量为G。若已知第一宇宙速度 =7.9k/s,地球半径R=6.4×103km,万有引力恒量G=6.67×10
=7.9k/s,地球半径R=6.4×103km,万有引力恒量G=6.67×10 N·m2·kg
N·m2·kg 。
。
求:(1)第一宇宙速度的计算式;
(2)地球的质量(要求保留两位有效数字)。
关于万有引力定律和引力常量的发现,下面说法中正确的是( )
| A.万有引力定律是由开普勒发现的,而引力常量是由伽利略测定的 |
| B.万有引力定律是开普勒发现的,而引力常量是由卡文迪许测定的 |
| C.万有引力定律是牛顿发现的,而引力常量是由胡克测定的 |
| D.万有引力定律是牛顿发现的,而引力常量是由卡文迪许测定的 |
两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R,其运动周期为T,求两星的总质量。
中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T= s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67
s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67 10
10 m
m /kg·s
/kg·s )
)
中国计划在2017年实现返回式月球软着陆器对月球进行科学探测,届时发射一颗运动半径为r的绕月卫星.登月着陆器从绕月卫星出发,沿椭圆轨道降落到月球的表面上,与月球表面经多次碰撞和弹跳才停下来.假设着陆器第一次弹起的最大高度为h,水平速度为v1,第二次着陆时速度为v2.已知月球半径为R,求:在月球表面发射人造月球卫星的最小发射速度.
宇宙飞船绕地心做半径为r的匀速圆周运动,飞船舱内有一质量为m的人站在可称体重的台秤上,用R表示地球的半径,g表示地球表面处的重力加速度,g0表示宇宙飞船所在处的地球引力加速度,N表示人对秤的压力,则关于g0、N下面正确的是 ( )
A.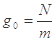 |
B.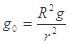 |
C.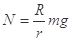 |
D. N=0 |
宇航员在一星球表面上的某高处,沿水平方向抛出一小球。经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时初速度增大到2倍,则抛出点与落地点之间的距离为 L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
设地球表面的重力加速度为g,物体在距地心4R(R是地球半径)处,由于地球的引力作用而产生的重力加速度g,,则g/g,为()
| A.1; | B.1/9; | C.1/4; | D.1/16。 |
如图所示,在距一质量为M、半径为R、密度均匀的球体中心2R处,有一质量为m的质点,M对m的万有引力的大小为F。现从M中挖出一半径为r的球体,如图,OO′=R/2。求M中剩下的部分对m的万有引力的大小。
在天文学中,把两颗相距较近的恒星叫双星,已知两恒星的质量分别为m和M,两星之间的距离为L,两恒星分别围绕共同的圆心作匀速圆周运动,如图所示,求恒星运动的半径和周期。
已知地球赤道上的物体随地球自转的线速度大小为v1,向心加速度大小为a1,近地卫星速度大小为v2,向心加速度大小为a2,地球同步卫星线速度大小为v3,向心加速度大小为a3,设近地卫星距地面高度不计,同步卫星距地面高度约为地球半径的6倍,则以下结论正确的是( )
A.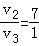 |
B.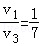 |
C.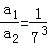 |
D.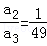 |
试题篮
()