2012年6月18 日,神舟九号飞船与天官一号目标发生器在离地面343km的近圆形轨道上成功进行了我国首次载人空间交会对接。对接轨道所处的空间存在极其稀薄的大气。下列说法正确的是( )
| A.为实现对接,两者运行速度都应介于第一宇宙速度和第二宇宙速度之间 |
| B.如不加干预,在运行一段时间后,天宫一号的动能可能会增加 |
| C.如不加干预,天宫一号的轨道高度将缓慢降低 |
| D.航天员在天宫一号中处于失重状态,说明航天员不受地球引力作用 |
发射地球同步卫星时,先将卫星发射至近地圆形轨道1,然后经点火使其沿椭圆轨道2运行,最后再次点火将卫星送入同步轨道3。轨道1、2相切于A点,轨道2、3相切于B点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
| A.卫星在轨道1上的运行速率大于轨道3上的速率 |
| B.卫星在轨道1上的角速度小于在轨道3上的角速度 |
| C.卫星在椭圆轨道2上经过A点时的速度大于7.9 km/s |
| D.卫星在椭圆轨道2上经过B点时的加速度等于它在轨道3上经过B点时的加速度 |
2012年4月30日4时50分,我国在西昌卫星发射中心用“长征三号乙”运载火箭,成功发射两颗北斗导航卫星. 这是我国首次采用“一箭双星”方式发射两颗地球中高轨道卫星. 北斗卫星导航系统由静止轨道卫星(同步卫星)和中轨道卫星组成,中轨道卫星平均分布在倾角55°的三个平面上,轨道高度约21500km,静止轨道卫星的高度约为36000km. 下列说法中正确的是
| A.在静止轨道上,卫星的质量越大其运行周期越小 |
| B.静止轨道卫星的线速度小于中轨道卫星的线速度 |
| C.中轨道卫星的周期一定大于24 h |
| D.中轨道卫星的线速度可能大于7.9km/s |
“嫦娥一号”的成功发射,为实现中华民族几千年的奔月梦想迈出了重要的一步.如图所示,“嫦娥一号”先进入绕月飞行的椭圆轨道,然后再椭圆轨道近月点 变轨进入绕月飞行圆轨道;已知“嫦娥一号”绕月飞行的椭圆轨道远月点
变轨进入绕月飞行圆轨道;已知“嫦娥一号”绕月飞行的椭圆轨道远月点 距月球表面高度为
距月球表面高度为 ;又已知“嫦娥一号”绕月圆轨道飞行时,距月球表面的高度为
;又已知“嫦娥一号”绕月圆轨道飞行时,距月球表面的高度为 ,飞行周期为
,飞行周期为 ,月球的半径为
,月球的半径为 ,万有引力常量为
,万有引力常量为 ;再后,假设宇航長在飞船上,操控飞船在月球表面附近竖直平面内俯冲,在最低点附近作半径为
;再后,假设宇航長在飞船上,操控飞船在月球表面附近竖直平面内俯冲,在最低点附近作半径为 的圆周运动,宇航员质量是
的圆周运动,宇航员质量是 ,飞船经过最低点时的速度是
,飞船经过最低点时的速度是 .求:
.求:
(1)月球的质量 是多大?
是多大?
(2)“嫦娥一号”经绕月飞行的椭圆轨道远月点 时的加速度多大?“嫦娥一号”经绕月飞行的椭圆轨道近月点
时的加速度多大?“嫦娥一号”经绕月飞行的椭圆轨道近月点 时欲变轨进入如图圆轨道,应该向前还是向后喷气?
时欲变轨进入如图圆轨道,应该向前还是向后喷气?
(3)操控飞船在月球表面附近竖直平面内俯冲经过最低点时,座位对宇航员的作用力 是多大?
是多大?
假设人造卫星绕地球做匀速圆周运动,当卫星绕地球运动的轨道半径增大到原来的2倍时,则有( )
| A.卫星运动的线速度将减小到原来的一半 |
| B.卫星所受的向心力将减小到原来的四分之一 |
| C.卫星运动的周期将增大到原来的2倍 |
D.卫星运动的线速度将减小到原来的 |
设想我国宇航员随“嫦娥”号登月飞船贴近月球表面做匀速圆周运动,宇航员测出飞船绕行n圈所用的时间为t。登月后,宇航员利用身边的弹簧秤测出质量为m的物体重力G1。已知引力常量为G,根据以上信息可得到
| A.月球的密度 |
| B.飞船的质量 |
| C.月球的第一宇宙速度 |
| D.月球的自转周期 |
2011年11月3日,“神州八号”飞船与“天宫一号”目标飞行器成功实施了首次交会对接。任务完成后“天宫一号”经变轨升到更高的轨道,等待与“神州九号”第二次交会对接.变轨前和变轨完成后“天宫一号”的运行轨道均可视为圆轨道,对应的轨道半径分别为 、
、 ,对应的角速度和向心加速度分别为
,对应的角速度和向心加速度分别为 、
、 和
和 、
、 ,则有( )
,则有( )
A. |
B. |
| C.变轨后的“天宫一号”比变轨前动能增大了,机械能增加了 |
| D.在正常运行的“天宫一号”内,体重计、弹簧测力计、天平都不能使用了 |
如图所示是中国嫦娥一号卫星发回的第一张月球表面照片,陨石落入月球表面形成的美丽“花环”清晰可见.如果大量的陨石落入(忽略碰撞引起的月球速度变化),使月球的质量增加,则 ( )
| A.月球的公转周期不变 |
| B.地月距离增大 |
| C.某月球卫星的线速度减小 |
| D.某月球卫星的周期减小 |
“嫦娥一号”探月卫星为绕月极地卫星.利用该卫星可对月球进行成像探测.设卫星在绕月极地轨道上做匀速圆周运动时距月球表面的高度为H,绕行周期为TM;月球绕地球公转的周期为TE,轨道半径为R0;地球半径为RE,月球半径为RM.已知光速为c.
(1)如图所示,当绕月极地轨道的平面与月球绕地球公转的轨道平面垂直时(即与地心到月心的连线垂直时),求绕月极地卫星向地球地面发送照片需要的最短时间;
(2)忽略地球引力、太阳引力对绕月卫星的影响,求月球与地球的质量之比.
物体在万有引力场中具有的势能叫做引力势能.若取两物体相距无穷远时的引力势能为零,则一个质量为m0的质点到质量为M0的引力源中心的距离为r0时,其万有引力势能为EP=-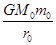 (式中G为万有引力常量).一颗质量为m的人造地球卫星沿轨道半径为r1的圆形轨道环绕地球做匀速圆周运动,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为:(假设卫星的质量始终不变,不计一切阻力及其它星体的影响)
(式中G为万有引力常量).一颗质量为m的人造地球卫星沿轨道半径为r1的圆形轨道环绕地球做匀速圆周运动,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为:(假设卫星的质量始终不变,不计一切阻力及其它星体的影响)
A.E= ( (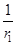 - -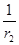 ) ) |
B.E=GMm(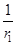 - -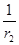 ) ) |
C.E=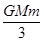 ( (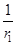 - -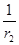 ) ) |
D.E=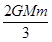 ( (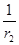 - -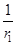 ) ) |
人造卫星绕地球只受地球的引力,做匀速圆周运动,其轨道半径为r,线速度为v,周期为T。为使其周期变为8T,可采用的方法有
| A.保持轨道半径不变,使线速度减小为v/8 |
| B.逐渐减小卫星质量,使轨道半径逐渐增大为4r |
| C.逐渐增大卫星质量,使轨道半径逐渐增大为8r |
| D.保持线速度不变v,将轨道半径增加到8r |
如图所示,“嫦娥一号”探月卫星进入月球轨道后,首先在椭圆轨道Ⅰ上运动,P、Q两点是轨道Ⅰ的近月点和远月点,Ⅱ是卫星绕月做圆周运动的轨道,轨道Ⅰ和Ⅱ在P点相切,关于该探月卫星的运动,下列说法正确的是
| A.卫星在轨道Ⅰ上运动周期大于在轨道Ⅱ上运动的周期 |
| B.卫星由轨道Ⅰ进入轨道Ⅱ必须要在P点加速 |
| C.卫星在轨道Ⅰ上运动时,P点的速度小于Q点的速度 |
| D.卫星在轨道Ⅰ上运动时,P点的加速度小于Q点的加速度 |
假设地球的卫星1和月球的卫星2,分别绕地球和月球做匀速圆周运动,如图所示,两颗卫星2的轨道半径相同。已知地球的质量大于月球的质量,两颗卫星相比较,下列说法中正确的是
| A.卫星1的向心加速度较小 |
| B.卫星1的动能较大 |
| C.卫星1的周期较小 |
| D.若卫星1是地球的同步卫星,则它的质量一定 |
两个行星各有一个卫星绕其表面运行,已知两个卫星的周期之比为1:3,两行星半径之比为3:1,则:
(1)两行星密度之比为多少?
(2)两行星表面处重力加速度之比为多少?
试题篮
()