一列简谐横波在弹性介质中沿x轴传播,波源位于坐标原点O,t=O时刻波源开始振动,t="3" s时波源停止振动,如图为t="3." 2 s时的波形图。其中质点a的平衡位置离原点O的距离为x=2.5m。以下说法正确的是_______。(选对一个给3分,选对两个给4分,选对3个给6分。每选错一个扣3分,最低得分为0分)
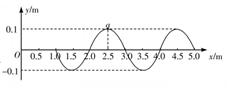
| A.波速为5m/s |
B.波长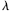 ="2.0" m ="2.0" m |
| C.波源起振方向沿y轴正方向 |
| D.在t=3.3 s,质点a位于波谷 |
E. 从波源起振开始计时,3.0 s内质点a运动的总路程为2. 5 m
如图所示,为一列水平向右传播的简谐横波在某一时刻的波形图,波速大小为0.6 m/s。P质点的平衡位置坐标为x=0.96m。从该时刻(图中状态,此时刻波从O点刚好向右传播了一个波长的距离)开始计时,问:
①经过多少时间,P质点第一次到达波峰?
②P质点第一次到达波峰时,通过的路程为多少?
如图所示,带电量分别为4q和-q的小球A、B固定在水平放置的光滑绝缘细杆上,相距为d.若杆上套一带电小环C,带电体A、B和C均可视为点电荷.
(1)求小环C的平衡位置.
(2)若小环C带电量为q,将小环拉离平衡位置一小位移x(|x|《d)后静止释放,试判断小环C能否回到平衡位置.(回答“能”或“不能”即可)
(3)若小环C带电量为-q,将小环拉离平衡位置一小位移x(|x|《d)后静止释放,试证明小环C将作简谐动.(提示:当α《1时,则 ≈1-nα)
≈1-nα)
在均匀介质中,各质点的平衡位置在同一直线上,相邻两质点问的距离均为s,如图所示。振动从质点1开始向右传播,质点l开始运动时的速度方向竖直向上。经过时间t,前13个质点第一次形成如图所示的波形。求:
(1)这列波的周期;
(2)这列波的传播速度。
一个物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时,位移为4 cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程.
一列简谐横波由质点A向质点B传播。已知A、B两点相距4m,这列波的波长大于2m而小于20m。上图表示在波的传播过程中A、B两质点的振动的图象。求波的传播速度。
一个小球和轻质弹簧组成的系统按x1=5 sin cm的规律振动.
cm的规律振动.
(1)求该振动的周期、频率、振幅和初相.
(2)另一简谐运动的表达式为x2=5 sin cm,求它们的相位差.
cm,求它们的相位差.
如图所示,A、B两物体的质量都为m,拉A的细线与水平方向的夹角为30°时,物体A、B处于静止状态,设弹簧的劲度系数为k;某时刻悬线突然断开,A在水平面上做周期为T的简谐运动,B自由下落,当B落地时,A恰好将弹簧压缩到最短,,不计一切摩擦阻力,求:
(1)A振动时的振幅;
(2)B落地时的速度.
如图,两根劲度系数分别为K1、K2的轻质弹簧与小球相连结,另外一端固定不动。整个装置位于光滑的水平地面上。当小球位于O点时,两弹簧均处于原长状态。今把小球沿弹簧轴线方向拉离O一小段距离后放手。证明小球此后的运动为简谐运动。
一列简潜横波,如图中的实线是某时刻的波形图象,虚线是经过0.2s时的波形图象。
①假定波向左传播,求它传播的可能距离;
②若这列波向右传播,求它的最大周期:
③假定波速是35m/s,求波的传播方向。
有两列简谐横波a、b在同一媒质中沿x轴正方向传播,波速均为v=2.5m/s。在t=0时,两列波的波峰正好在x=2.5m处重合,如图所示。
(1)求两列波的周期Ta和Tb。
(2)求t=0时,两列波的波峰重合处的所有位置。
如图所示, \倾角为 的斜面体(斜面光滑且足够长)固定在水平地面上,斜面顶端与劲度系数为
的斜面体(斜面光滑且足够长)固定在水平地面上,斜面顶端与劲度系数为 、自然长度为
、自然长度为 的轻质弹簧相连,弹簧的另一端连接着质量为
的轻质弹簧相连,弹簧的另一端连接着质量为 的物块。压缩弹簧使其长度为
的物块。压缩弹簧使其长度为 时将物块由静止开始释放(物快做简谐运动),且物块在以后的运动中,斜面体始终处于静止状态。重力加速度为
时将物块由静止开始释放(物快做简谐运动),且物块在以后的运动中,斜面体始终处于静止状态。重力加速度为 。
。
(1)求物块处于平衡位置时弹簧的长度;
(2)物块做简谐运动的振幅是多少;
(3)选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标轴,用 表示物块相对于平衡位置的位移,证明物块做简谐运动;(已知做简谐运动的物体所受的恢复力满足 F=—kx)
表示物块相对于平衡位置的位移,证明物块做简谐运动;(已知做简谐运动的物体所受的恢复力满足 F=—kx)
如图所示,质量为m=0.5kg的物体放在质量为M=4.5kg的平台上,随平台上、下做简谐运动.设在简谐运动过程中,二者始终保持相对静止.已知弹簧的劲度系数为k=400N/m,振幅为A=0.1m. 试求:二者一起运动到最低点时,物体对平台的压力大小 (取g=10m/s)
如图所示,质量为m的砝码A放置在质量为M的滑块B上,B与弹簧相连,它们一起在光滑的水平面上作简谐运动,弹簧的劲度系数为k,砝码与滑块之间的动摩擦因数为 ,要使砝码与滑块在振动过程中不发生相对运动,问最大振幅等于多少?(设最大静摩擦力等于滑动摩擦力)
,要使砝码与滑块在振动过程中不发生相对运动,问最大振幅等于多少?(设最大静摩擦力等于滑动摩擦力)
试题篮
()