如图所示,两气缸AB粗细均匀,等高且内壁光滑,其下部由体积可忽略的细管连通;A的直径为B的2倍,A上端封闭,B上端与大气连通;两气缸除A顶部导热外,其余部分均绝热。两气缸中各有一厚度可忽略的绝热轻活塞a、b,活塞下方充有氮气,活塞a上方充有氧气;当大气压为P0,外界和气缸内气体温度均为7℃且平衡时,活塞a离气缸顶的距离是气缸高度的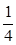 ,活塞b在气缸的正中央。
,活塞b在气缸的正中央。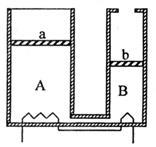
(ⅰ)现通过电阻丝缓慢加热氮气,当活塞b升至顶部时,求氮气的温度;
(ⅱ)继续缓慢加热,使活塞a上升,当活塞a上升的距离是气缸高度的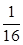 时,求氧气的压强。
时,求氧气的压强。
如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体。活塞的质量为m,横截面积为S,与容器底部相距h。现通过电热丝缓慢加热气体,当气体的温度为T1时活塞上升了h。已知大气压强为p0。重力加速度为g,不计活塞与气缸间摩擦。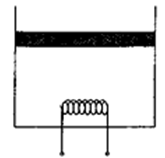
i.求温度为T1时气休的压强;
ii.现停止对气体加热,同时在活塞上缓慢添加砂粒,当添加砂粒的质量为m0时,活塞恰好回到原来位置,求此时气体的温度
如图(a)所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积S=2×10 -3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P0=1.0×105Pa。现将气缸竖直放置,如图(b)所示,取g=10m/s2。求: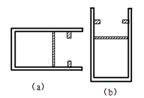
①活塞与气缸底部之间的距离;
②加热到675K时封闭气体的压强。
如图所示,内壁光滑的气缸竖直放置,在距气缸底部l=36cm处有一与气缸固定连接的卡环,活塞与气缸底部之间封闭了一定质量的气体。当气体的温度 T1=300K、大气压强 P0=1.0×105Pa时,活塞与气缸底部之间的距离l0=30cm,已知活塞面积为50cm2,不计活塞的质量和厚度。现对缸内气体加热,使活塞缓慢上升,当温度上升至T2=540K时,求: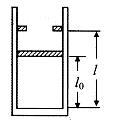
①封闭气体此时的压强;②该过程中气体对外做的功。
如图所示,一定质量的理想气体从状态A经等压过程到状态B。此过程中,气体压强p=1.0×105Pa,吸收的热量Q=7.0×102J, 求此过程中气体内能的增量。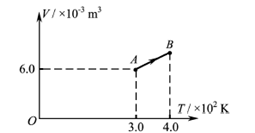
如图所示,一根粗细均匀的细玻璃管开口朝上竖直放置,玻璃管中有一段长为h = 24cm的水银柱封闭了一段长为x0 = 23cm的空气柱,系统初始温度为T0 = 200K,外界大气压恒定不变为P0 = 76cmHg。现将玻璃管开口封闭,将系统温度升至T = 400K,结果发现管中水银柱上升了2cm。若空气可以看作理想气体,求升温后玻璃管内封闭的上下两部分空气的压强分别为多少?
))如图(a)所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2×10 3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P0=1.0×105Pa。现将气缸竖直放置,如图(b)所示,取g=10m/s2。求:
①活塞与气缸底部之间的距离;
②加热到675K时封闭气体的压强。
如图所示,静止的气缸内封闭了一定质量的气体,水平轻杆一端固定在墙壁上,另一端与气缸内的活塞相连。已知大气压强为1.0×105Pa,气缸的质量为50kg,活塞质量不计,其横截面积为0.01m2,气缸与地面间的最大静摩擦力为气缸重力的0.4倍,活塞与气缸之间的摩擦可忽略。开始时被封闭气体压强为1.0×105Pa、温度为27℃,试求:
(1)缓慢升高气体温度,气缸恰好开始向左运动时气体的压强P和温度t;
(2)某同学认为封闭气体的温度只有在27C到(1)问中t之间,才能保证气缸静止不动,你是否同意他的观点?若同意,请说明理由;若不同意,计算出正确的结果。
一活塞将一定质量的理想气体封闭在汽缸内,初始时气体体积为3.0×10-3 m3,测得此时气体的温度和压强分别为300 K和1.0×105 Pa,加热气体缓慢推动活塞,测得气体的温度和压强分别为320 K和1.0×105 Pa。
①求此时气体的体积。
②保持温度为320 K不变,缓慢改变作用在活塞上的力,使气体压强变为8.0×104 Pa,求此时气体的体积。
一定质量的理想气体被活塞封闭在竖直放置的圆柱形气缸内,汽缸壁导热良好,活塞可沿气缸壁无摩擦地滑动。开始时气体压强为p,活塞下表面相对于气缸底部的高度为h,外界温度为T0。现取质量为m的沙子缓慢地倒在活塞的上表面,沙子倒完时,活塞下降了h/4.若此后外界的温度变为T,求重新到达平衡后气体的体积。已知外界大气的压强始终保持不变,重力加速度大小为g。
(12分)如图所示,柱形容器内用不漏气的轻质绝热活塞封闭一定量的理想气体,容器外包裹保温材料。开始时活塞至容器底部的高度为H1,容器内气体温度与外界温度相等.在活塞上逐步加上多个砝码后,活塞下降到距容器底部H2处,气体温度升高了ΔT;然后取走容器外的保温材料,活塞位置继续下降,最后静止于距容器底部H3处,已知大气压强为p0.求气体最后的压强与温度.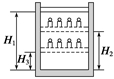
如图所示,一密闭的截面积为S的圆筒形汽缸,高为H,中间有一薄活塞,用一劲度系数为k的轻弹簧吊着,活塞重为G,与汽缸紧密接触,不导热且气体是同种气体,且质量、温度、压强都相同时,活塞恰好位于汽缸的正中央,设活塞与汽缸壁间的摩擦可不计,汽缸内初始压强为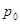 ,温度为
,温度为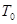 。求:
。求: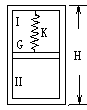
(1)弹簧原长
(2)如果将汽缸倒置,保持汽缸Ⅱ部分的温度不变,使汽缸Ⅰ部分升温,使得活塞在汽缸内的位置不变,则汽缸Ⅰ部分气体的温度升高多少?
如图(a)所示,内壁光滑、粗细均匀、左端封闭的玻璃管水平放置。横截面积S=2.0×10-5m2的活塞封闭一定质量的气体,气柱长度l0=20cm,压强与大气压强相同。缓慢推动活塞,当气柱长度变为l=5cm时,求:(大气压强p0=1.0×105Pa,环境温度保持不变)
(1)玻璃管内气体的压强p
(2)作用在活塞上的推力大小F
(3)在图(b)中画出推动活塞过程中,气体经历的状态变化过程
气筒给自行车打气时,每打一次都把压强1个标准大气压、温度为27℃、体积为112mL空气的打进车胎。求该气筒每打一次气时,进入车胎内空气分子的个数。已知1 mol 空气在 1个标准大气压、0℃ 时的体积为 22.4 L,阿伏加德罗常数NA= 6×1023mol-1。(计算结果保留一位有效数字)
试题篮
()