如图所示,一竖直放置的、长为L的细管下端封闭,上端与大气(视为理想气体)相通,初始时管内气体温度为 。现用一段水银柱从管口开始注入管内将气柱封闭,该过程中气体温度保持不变且没有气体漏出,平衡后管内上下两部分气柱长度比为l∶3。若将管内下部气体温度降至
。现用一段水银柱从管口开始注入管内将气柱封闭,该过程中气体温度保持不变且没有气体漏出,平衡后管内上下两部分气柱长度比为l∶3。若将管内下部气体温度降至 ,在保持温度不变的条件下将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出)。已知
,在保持温度不变的条件下将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出)。已知 ,大气压强为
,大气压强为 ,重力加速度为g。求水银柱的长度h和水银的密度
,重力加速度为g。求水银柱的长度h和水银的密度 。
。
如图所示,A、B气缸的长度均为60cm,截面积均为40cm2,C是可在气缸内无摩擦滑动的、体积不计的活塞,D为阀门。整个装置均由导热材料制成。原来阀门关闭,A内有压强PA=2.4×105Pa的氧气.B内有压强PB=1.2×105Pa的氢气。阀门打开后,活塞C向右移动,最后达到平衡.求:
Ⅰ.活塞C移动的距离及平衡后B中气体的压强;
Ⅱ.活塞C移动过程中B中气体是吸热还是放热(简要说明理由)。
(假定氧气和氢气均视为理想气体,连接气缸的管道体积可忽略)
如图,竖直平面内有一直角形内径相同的 细玻璃管,A端封闭,C端开口,AB="BC" =l0,且此时A、C端等高。管内水银总长度为l0,玻璃管AB内封闭长为l0/2的空气柱。已知大气压强为l0汞柱髙。如果使玻璃管绕B点在竖直平面内顺时针缓慢地转动至BC管水平,求此时AB管内气体 的压强为多少汞柱高?管内封入的气体可视为理想气体且温度不变。
如图所示,一直立的汽缸用一质量为m的活塞封闭一定质量的理想气体,活塞横截面积为S,气体最初的体积为V0,气体最初的压强为p0/2,汽缸内壁光滑且缸壁是导热的。开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,设周围环境温度保持不变,已知大气压强为p0,重力加速度为g。若一定质量理想气体的内能仅由温度决定,求: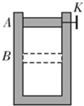
①活塞停在B点时缸内封闭气体的体积V;
②整个过程中通过缸壁传递的热量Q。
如图所示,一直立的汽缸用一质量为m的活塞封闭一定质量的理想气体,活塞横截面积为S,气体最初的体积为V0,气体最初的压强为p0/2,汽缸内壁光滑且缸壁是导热的。开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,设周围环境温度保持不变,已知大气压强为p0,重力加速度为g。若一定质量理想气体的内能仅由温度决定,求: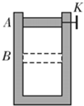
①活塞停在B点时缸内封闭气体的体积V;
②整个过程中通过缸壁传递的热量Q。
如图所示,用销钉固定的光滑绝热活塞把水平放置的绝热气缸分隔成容积相同的A、B两部分,A、B缸内分别封闭有一定质量的理想气体。初始时,两部分气体温度都为t0=27℃,A部分气体压强为pA0=2×105Pa,B部分气体压强为pB0=1×105Pa。拔去销钉后,保持A部分气体温度不变,同时对B部分气体加热,直到B内气体温度上升为t=127℃,停止加热,待活塞重新稳定后,(活塞厚度可忽略不计,整个过程无漏气发生)求: 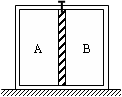
(1)A部分气体体积与初始体积之比VA:VA0;
(2)B部分气体的压强pB。
一定质量的理想气体体积V与热力学温度T的关系图象如图所示,气体在状态A时的压强P0=1.0×105 Pa,线段AB与V轴平行。
(1)求状态B时的压强为多大?
(2)气体从状态A变化到状态B过程中,对外界做的功为10 J,求该过程中气体吸收的热量为多少?
如图所示,在一圆形管道内封闭有理想气体,用一固定活塞K和不计质量可自由移动的活塞A,将管内气体分割成体积相等的两部分。固定活塞K、可动活塞A和管道中心O处于同一水平线上。管道内气体温度都为T0=300K,压强都为P0=1.0×105Pa。现保持管道下部分气体温度不变,只对管道上部分气体缓慢加热,当可动活塞P缓慢移动到管道最低点时(不计摩擦),求;
①下部分气体的压强;
②上部分气体的温度。
如图所示,两端开口、粗细均匀的足够长玻璃管插在大水银槽中,管的上部有一定长度的水银,两段空气柱被封闭在左右两侧的竖直管中.开启上部连通左右水银的阀门A,当温度为300 K平衡时水银的位置如图,其中左侧空气柱长度L1=50cm,左侧空气柱底部的水银面与水银槽液面高度差为h2=5cm,左右两侧顶部的水银面的高度差为h1=5cm,大气压为75 cmHg。求: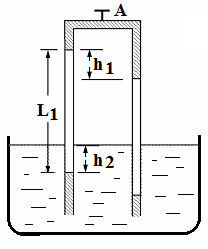
①右管内气柱的长度L2,
②关闭阀门A,当温度升至405 K时,左侧竖直管内气柱的长度L3.
(1)在“用油膜法估测分子的大小”的实验中,若100滴油酸的体积为1ml,则1滴油酸所能形成的单分子油膜的面积约是 .(油酸的摩尔质量M=0.283kg·mol-1,密度ρ=0.895×103kg·m-3,NA=6.02×1023mol-1.结果保留一位有效数)
(2)如图所示,两端开口、粗细均匀的足够长玻璃管插在大水银槽中,管的上部有一定长度的水银,两段空气柱被封闭在左右两侧的竖直管中.开启上部连通左右水银的阀门A,当温度为300 K平衡时水银的位置如图,其中左侧空气柱长度L1=50cm,左侧空气柱底部的水银面与水银槽液面高度差为h2=5cm,左右两侧顶部的水银面的高度差为h1=5cm,大气压为75 cmHg.求: 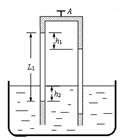
①右管内气柱的长度L2
②关闭阀门A,当温度升至405 K时,左侧竖直管内气柱的长度L3
如图,一定质量的理想气体被不计质量的活塞封闭在可导热的气缸内,活塞距底部的高度为h,可沿气缸无摩擦地滑动。取一小盒沙子缓慢地倒在活塞的上表面上,沙子倒完时,活塞下降了h/5。再取相同质量的一小盒沙子缓慢地倒在活塞的上表面上。外界大气的压强和温度始终保持不变,已知大气压为p0,活塞横截面积为S,重力加速度为g,求:
(1)一小盒沙子的质量;
(2)沙子再次倒完时活塞距气缸底部的高度。
水的沸点与水面上方气压有关,气压越大水的沸点越高。下表给出了水面上方气体压强与沸点的对应关系。技术员小陈利用这一关系,设计了如图所示的锅炉水温控制装置:图中OC为一可绕O点旋转的横杆(质量不计),在横杆上的B点下方连接着阀门S,阀门的底面积为3cm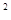 ,OB长度为20cm,横杆上A点处挂着重物G,OA长度为60cm。对水加热时,随着水温升高,水面上方气压增大,当压强增大到一定值时,阀门S被顶开,使锅炉内气体压强减小,水开始沸腾。当重物G挂在不同位置时,锅炉内水面上方气体压强可达到的最大值不同,从而控制锅炉内水的最高温度。
,OB长度为20cm,横杆上A点处挂着重物G,OA长度为60cm。对水加热时,随着水温升高,水面上方气压增大,当压强增大到一定值时,阀门S被顶开,使锅炉内气体压强减小,水开始沸腾。当重物G挂在不同位置时,锅炉内水面上方气体压强可达到的最大值不同,从而控制锅炉内水的最高温度。
(1)当锅炉内水的温度达到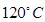 沸腾时,锅炉内气体的压强是多少?
沸腾时,锅炉内气体的压强是多少?
(2)当大气压强为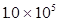 Pa时,将G挂在A位置,锅炉内水沸腾时的温度为
Pa时,将G挂在A位置,锅炉内水沸腾时的温度为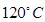 ,求此时阀门底部受到的气体压力和上部受到的大气压力的差值是多少?(计算时可认为阀门上、下底面积相等)
,求此时阀门底部受到的气体压力和上部受到的大气压力的差值是多少?(计算时可认为阀门上、下底面积相等)
(3)当大气压强为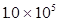 Pa时,要使锅炉内水的温度达到
Pa时,要使锅炉内水的温度达到 时沸腾,应将G挂在离O点多远处?
时沸腾,应将G挂在离O点多远处?
| 压强(Pa) |
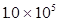 |
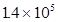 |
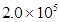 |
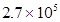 |
沸点(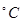 ) ) |
100 |
110 |
120 |
130 |
内径均匀的U型管中装有水银,两管中水银面与管口的距离均为l=10cm,大气压强p0=75.8cmHg,现将右管口封闭,如图所示,然后从左侧管口处将一活塞缓慢向下推入管中,直到左右两侧水银面高度差h=6cm时为止,求活塞在左管内移动的距离。(设整个过程温度不变)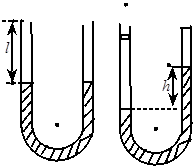
把一根两端开口带有活塞的直管的下端浸入水中,活塞开始时刚好与水面平齐,现将活塞缓慢地提升到离水面H=15m高处,如图所示,求在这过程中外力做功为多少?(已知活塞面积S=1.0dm2,大气压户p0=1.0×105Pa,活塞的厚度和质量不计,取g=10m/s2)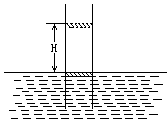
如图所示,绝热隔板S把绝热的气分隔成体积相等的两部分,S与气缸壁的接触是光滑的.两部分中分别盛有相同质量、相同温度的同种气体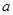 和
和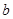 ,气体分子之间相互作用可忽略不计.现通过电热丝对气体
,气体分子之间相互作用可忽略不计.现通过电热丝对气体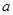 缓慢加热一段时间后,
缓慢加热一段时间后,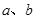 各自达到新的平衡状态.试分析气体
各自达到新的平衡状态.试分析气体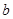 的压强、温度、内能的变化情况.
的压强、温度、内能的变化情况.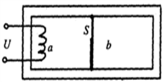
试题篮
()