工厂里有一种运货的过程可以简化为如图所示,货物以 的初速度滑上静止的货车的左端,已知货物质量m=20kg,货车质量M=30kg,货车高h=0.8m。在光滑轨道OB上的A点设置一固定的障碍物,当货车撞到障碍物时会被粘住不动,而货物就被抛出,恰好会沿BC方向落在B点。已知货车上表面的动摩擦因数
的初速度滑上静止的货车的左端,已知货物质量m=20kg,货车质量M=30kg,货车高h=0.8m。在光滑轨道OB上的A点设置一固定的障碍物,当货车撞到障碍物时会被粘住不动,而货物就被抛出,恰好会沿BC方向落在B点。已知货车上表面的动摩擦因数 ,货物可简化为质点,斜面的倾角为
,货物可简化为质点,斜面的倾角为 。
。
(1)求货物从A点到B点的时间;
(2)求AB之间的水平距离;
(3)若已知OA段距离足够长,导致货物在碰到A之前已经与货车达到共同速度,则货车的长度是多少?
(原创)某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示,光滑轨道中间部分水平,右侧为位于竖直平面内半径为R的半圆,在最低点与直轨道相切.5个大小相同、质量不等的小球并列静置于水平部分,球间有微小间隔,从左到右,球的编号依次为0、1、2、3、4,球的质量依次递减,每球质量与其相邻左球质量之比为k(k<1).将0号球向左拉至左侧轨道距水平高h处,然后由静止释放,使其与1号球碰撞,1号球再与2号球碰撞……所有碰撞皆为无机械能损失的正碰(不计空气阻力,小球可视为质点,重力加速度为g).
(1)0号球与1号球碰撞后,1号球的速度大小v1;
(2)若已知h=0.1m,R=0.64m,要使4号球碰撞后能过右侧轨道的最高点,问k值为多少?
如图所示,质量为M=0.5kg、长L=1m的平板车B静止在光滑水平面上,小车左端紧靠一半径为R=0.8m的光滑四分之一圆弧,圆弧最底端与小车上表面相切,圆弧底端静止一质量为mC=1kg的滑块.现将一质量为mA=1kg的小球从圆弧顶端静止释放,小球到达圆弧底端后与C发生弹性碰撞.C与B之间的动摩擦因数μ=0.2,取g=10m/s2.若在C刚好滑上木板B上表面的同时,给B施加一个水平向右的拉力F.试求: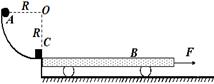
(1)滑块C滑上B的初速度v0.
(2)若F=2N,滑块C在小车上运动时相对小车滑行的最大距离.
(3)如果要使C能从B上滑落,拉力F大小应满足的条件.
在许多建筑工地经常使用打夯机将桩料打入泥土中以加固地基。打夯前先将桩料扶起、使其缓慢直立进入泥土中,每次卷扬机都通过滑轮用轻质钢丝绳将夯锤提升到距离桩顶 =5m处再释放,让夯锤自由下落,夯锤砸在桩料上并不弹起,而随桩料一起向下运动。设夯锤和桩料的质量均为m="500" kg,泥土对桩料的阻力为
=5m处再释放,让夯锤自由下落,夯锤砸在桩料上并不弹起,而随桩料一起向下运动。设夯锤和桩料的质量均为m="500" kg,泥土对桩料的阻力为 ,其中常数
,其中常数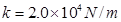 ,
, 是桩料深入泥土的深度。卷扬机使用电动机来驱动,卷扬机和电动机总的工作效率为
是桩料深入泥土的深度。卷扬机使用电动机来驱动,卷扬机和电动机总的工作效率为 =95%,每次卷扬机需用20 s的时间提升夯锤。提升夯锤时忽略加速和减速的过程,不计夯锤提升时的动能,也不计滑轮的摩擦。夯锤和桩料的作用时间极短,g取10
=95%,每次卷扬机需用20 s的时间提升夯锤。提升夯锤时忽略加速和减速的过程,不计夯锤提升时的动能,也不计滑轮的摩擦。夯锤和桩料的作用时间极短,g取10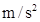 ,求:
,求: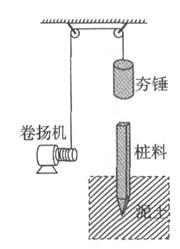
(1)在提升夯锤的过程中,电动机的输入功率;(结果保留2位有效数字)
(2)打完第一夯后,桩料进入泥土的深度。
如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,即F=-kx,其中k是由系统本身特性决定的线性回复力常数,那么质点的运动就是简谐运动。
(1)图1所示为一理想单摆,摆球的质量为m,摆长为L。重力加速度为g。请通过计算说明该单摆做简谐运动的线性回复力常数k=?
(2)单摆做简谐运动的过程中,由于偏角很小,因此可以认为摆球沿水平直线运动。
如图2所示,质量为m的摆球在回复力F=-kx作用下沿水平的x轴做简谐运动,若振幅为A,在平衡位置O点的速度为vm,试证明: 。
。
(3)如图3所示,两个相同的理想单摆均悬挂在P点。将B球向左拉开很小的一段距离由静止释放,B球沿水平的x轴运动,在平衡位置O点与静止的C球发生对心碰撞,碰撞后B、C粘在一起向右运动。已知摆球的质量为m,摆长为L。释放B球时的位置到O点的距离为d。重力加速度为g。求B、C碰撞后它们沿x轴正方向运动的最大距离。
如图所示,固定的光滑圆弧面与质量为6 kg的小车C的上表面平滑相接,在圆弧面上有一个质量为2 kg的滑块A,在小车C的左端有一个质量为2 kg的滑块B,滑块A与B均可看做质点.现使滑块A从距小车的上表面高h=1.25 m处由静止下滑,与B碰撞后瞬间粘合在一起共同运动,最终没有从小车C上滑出.已知滑块A、B与小车C的动摩擦因数均为μ=0.5,小车C与水平地面的摩擦忽略不计,取g=10 m/s2.求:
(1)滑块A与B碰撞后瞬间的共同速度的大小;
(2)小车C上表面的最短长度.
如图示,滑板A放在水平面上,长度为 ,滑块质量mA=1 kg、mB=0.99 kg,A、B间粗糙,现有mC="0.01" kg子弹以V0=200m/s速度向右击中B并留在其中,求
,滑块质量mA=1 kg、mB=0.99 kg,A、B间粗糙,现有mC="0.01" kg子弹以V0=200m/s速度向右击中B并留在其中,求
(1)子弹C击中B后瞬间,B速度多大
(2)若滑块A与水平面固定,B被子弹击中后恰好滑到A右端静止,求滑块B与A间动摩擦因数μ
(3)若滑块A与水平面光滑,B与A间动摩擦因数不变,试分析B能否离开啊, 并求整个过程A、B、C组成的系统损失的机械能
(18分)如图所示,半径R=1m的四分之一光滑圆轨道最低点D的切线沿水平方向,水平地面上紧靠轨道依次排放两块完全相同的木板A、B,长度均为L=2m,质量均为m2=1kg,木板上表面与轨道末端相切.质量m1=lkg的小物块(可视作质点)自圆轨道末端C点的正上方H=0.8m高处的A点由静止释放,恰好从C点切入圆轨道。物块与木板间的动摩擦因数为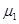 ,木板与水平地面间的动摩擦因数
,木板与水平地面间的动摩擦因数 =0.2,重力加速度为g=l0m/s
=0.2,重力加速度为g=l0m/s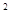 ,最大静摩擦力与滑动摩擦力相等。
,最大静摩擦力与滑动摩擦力相等。
(1)求物块到达圆轨道最低点D时所受轨道的支持力多大。
(2)若物块滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求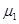 应满足的条件。
应满足的条件。
(3)若地面光滑,物块滑上木板后,木板A、 B最终共同运动,求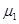 应满足的条件。
应满足的条件。
如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂,摆长相同,均为l。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,摆至最低点与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场,已知由于磁场的阻尼作用,金属球总能在下一次碰撞前停在最低点处,重力加速度为g。求:
(1)第一次碰撞前绝缘球的速度v0;
(2)第一次碰撞后绝缘球的速度v1;
(3)经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于37°
(你可能用到的数学知识:sin37°=0.6,cos37°=0.8,0.812=0.656,0.813=0.531,0.814=0.430,0.815=0.349,0.816=0.282)
)质量为M="6" kg的木板B静止于光滑水平面上,物块A质量为6 kg,停在B的左端。质量为1 kg的小球用长为0. 8 m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2 m,物块与小球可视为质点,不计空气阻力。已知A、B间的动摩擦因数 ,为使A、B达到共同速度前A不滑离木板,木板至少多长?
,为使A、B达到共同速度前A不滑离木板,木板至少多长?
如图所示,足够长的木板B静止在光滑水平地面上.小滑块A静止放在木板B的左端,已知mA=1kg、mB=2kg、滑块A与木板B间的动摩擦因数 ,现对小滑块A施加一个竖直平面内斜向右上方大小为10N的外力F,且F作用3s后撤去.若图中
,现对小滑块A施加一个竖直平面内斜向右上方大小为10N的外力F,且F作用3s后撤去.若图中 ,问:
,问:
(1)施加外力F时,滑块A及木板B加速度大小分别为多少?
(2)最终滑块A、木板B会一起在光滑水平面上做匀速运动,它们匀速运动的速度为多少?
(3)整个过程A、B组成的系统由于摩擦产生的内能是多少?
如图所示,在足够高的光滑水平台面上静置一质量为m的木板A,在木板的右端静置一质量为4m可视为质点的小物体B,A、B间的滑动摩擦系数μ = 0.25,且认为最大静摩擦力等于滑动摩擦力.离A右端足够远的平台边缘有一光滑定滑轮,用不可伸长的轻绳绕过定滑轮连接A和质量也为m的物体C,现由静止释放C,当它自由下落L时轻绳绷紧.当B与A相对静止时刚好到达A的左端.若重力加速度为g,不计空气阻力,不考虑A 与滑轮碰撞及之后的情形.
(1)求轻绳绷紧后瞬间物体C的速度大小;
(2)求木板A的长度;
(3)若物体B带有一定量的正电,其电荷量恒为q,轻绳刚绷紧的瞬间在空间加一水平向右的匀强电场,在保证物体B能滑离木板A的情况下求A、B间摩擦生热的最大极限值.
如图所示,有一竖直固定在地面的透气圆筒,筒中有一轻弹簧,其下端固定,上端连接一质量为m的薄滑块,当滑块运动时,圆筒内壁对滑块有阻力的作用,阻力的大小恒为Ff=mg(g为重力加速度).在初始位置滑块静止,圆筒内壁对滑块的阻力为零,弹簧的长度为l.现有一质量也为m的物体从距地面2l处自由落下,与滑块发生碰撞,碰撞时间极短.碰撞后物体与滑块粘在一起向下运动,运动到最低点后又被弹回向上运动,滑动到刚发生碰撞位置时速度恰好为零,不计空气阻力。求
(1)物体与滑块碰撞后共同运动速度的大小;
(2)下落物体与薄滑块相碰过程中损失的机械能多大。
(2)碰撞后,在滑块向下运动的最低点的过程中弹簧弹性势能的变化量。
如图示,水平面光滑,轻质弹簧右端固定,左端栓连物块b,小车质量M=3kg,粗糙部分AO长L=2m,动摩擦因数μ=0.3,OB部分光滑。另一小物块a,放在车的最左端,和车一起以v0=4m/s的速度向右匀速运动,车撞到固定挡板后瞬间速度变为零,但不与挡板粘连。已知车OB部分的长度大于弹簧的自然长度,弹簧始终处于弹性限度内。a、b 两物块视为质点质量均为m=1kg,碰撞时间极短且不粘连,碰后一起向右运动。(取g="10" m/s2)求:
(1)物块a与b碰前的速度大小
(2)弹簧具有的最大弹性势能
(3)当物块a相对小车静止时在小车上的位置距O点多远
(4)当物块a相对小车静止时小车右端B距挡板多远
如图所示,高H=1.6m的赛台ABCDE固定于地面上,其上表面ABC光滑;质量M=1kg、高h=0.8m、长L的小车Q紧靠赛台右侧CD面(不粘连),放置于光滑水平地面上.质量m =1kg的小物块P从赛台顶点A由静止释放,经过B点的小曲面无损失机械能的滑上BC水平面,再滑上小车的左端.已知小物块与小车上表面的动摩擦因数μ=0.4,g取10m/s2.
(1)求小物块P滑上小车左端时的速度v1。
(2)如果小物块没有从小车上滑脱,求小车最短长度L0 。
(3)若小车长L=1.2m,距离小车右端S处有与车面等高的竖直挡板,小车碰上挡板后立即停止不动,讨论小物块在小车上运动过程中,克服摩擦力做功Wf与S的关系。
试题篮
()