质量为1kg的小球以4m/s的速度与质量为2kg的静止小球正碰,碰撞后的速度可能是
A. m/s, m/s, m/s m/s |
B.-1m/s,2.5m/s | C.1m/s,1.5m/s | D.-4m/s,4m/s |
如图所示,A、B两物体彼此接触静止于光滑的水平桌面上,物体A的上表面是半径为R的光滑圆形轨道,物体C由静止开始从A上圆形轨道的右侧最高点下滑,则有( )
A.A和B不会出现分离现象
B.当C第一次滑到圆弧最低点时,A和B开始分离
C.A将会在桌面左边滑出
D.A不会在桌面上滑出
如图所示,在光滑的水平面上,有一质量为M=3kg的木板,木板上有质量为m=1kg的物块.它们都以v=4m/s的初速度反向运动,它们之间有摩擦,且木板足够长,当木板的速度为2.4m/s时,物块的运动情况是( )
| A.做加速运动 | B.做减速运动 |
| C.做匀速运动 | D.以上运动都有可能 |
如图所示,在光滑的水平面上,有一质量为M=3kg的薄板和质量 m=1kg的物块,都以v=4m/s的初速度朝相反方向运动,它们之间有摩擦,当薄板的速度为2.4m/s时,物块的运动情况是( )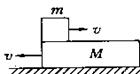
| A.做加速运动 | B.做减速运动 |
| C.做匀速运动 | D.以上运动都有可能 |
质量均为m的A、B两船静止在湖面上,设水对船的阻力不计,今A船上有一质量为m/2的人以水平速度v从A船跳到B船上,则A、B两船的速度大小之比( )
A.2:1 B.3:2 C.2:3 D.1:2
关于动量和动能,以下说法正确的是( )
| A.系统动量守恒的过程动能必定也守恒 |
| B.系统动能守恒的过程动量必定也守恒 |
| C.如果一个物体的动量保持不变,那么它的动能必然也保持不变 |
| D.如果一个物体的动能保持不变,那么它的动量必然也保持不变 |
两个物体质量分别为m1和m2,它们与水平面间的动摩擦因数分别为μ1和μ2,开始时弹簧被两个物体压缩后用细线拉紧,如图所示,当烧断细线时,被压缩的弹簧弹开的两物体可以脱离弹簧,则 ( )
| A.由于有摩擦力,所以系统动量一定不守恒 |
B.当 = =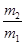 时,弹开过程中系统动量守恒 时,弹开过程中系统动量守恒 |
| C.m1和m2在刚脱离弹簧时的速度最大 |
| D.在刚烧断细线的瞬间,m1和m2的加速度一定最大 |
在如图所示的装置中,木块B与水平面间的接触面是光滑的,子弹A沿水平方向向射入木块后并留在木块内,将弹簧压缩到最短。现将木块、弹簧、子弹合在一起作为研究对象,则此系统在从子弹开始射入到弹簧压缩到最短的过程中 ( )
| A.动量守恒,机械能守恒 |
| B.动量不守恒,机械能不守恒 |
| C.动量守恒,机械能不守恒 |
| D.动量不守恒,机械能守恒 |
如图所示,木块A放在木块B的左上端,两木块间的动摩擦因数为μ。用水平恒力F将木块A拉至B的右端,第一次将B固定在地面上,F做的功为W1,系统产生的热量为Q1;第二次让B可以在光滑地面上自由滑动,F做的功为W2,系统产生的热量为Q2,判断正确的是:
| A.W1<W2 | B.W1>W2 |
| C.Q1<Q2 | D.Q1>Q2 |
甲乙两船质量均为M,以相同的速率v相向而行。甲船上站着一个质量为m的人随船行驶,不计水的阻力,当他由甲船跳上乙船,再由乙船跳回到甲船上,这样反复几次后,乙船速度变为零,则甲船的速度为( )
| A.mv/(M+m) | B.(2M+m)v/(M+m) |
| C.0 | D.mv/(2M+m) |
一个静止的放射性原子核发生天然衰变时,在匀强磁场中得到内切圆的两条路径1、2,如图所示,两圆半径之比为44∶1,则:
| A.发生的是α衰变 |
| B.轨迹2是反冲核的径迹 |
| C.反冲核是逆时针运动,放射出的粒子是顺时针运动 |
| D.该放射性元素的原子序数是90 |
将一个质量为3 kg的木板置于光滑水平面上,另一质量为1 kg的物块放在木板上.已知物块和木板间有摩擦,而木板足够长,若两者都以大小为4 m/s的初速度向相反方向运动(如上图),则当木板的速度为2.4 m/s时,物块正在( )
| A.水平向左匀减速运动 | B.水平向右匀加速运动 |
| C.水平方向做匀速运动 | D.处于静止状态 |
质量相等的三个小球 、
、 、
、 在光滑的水平面上以相同的速度运动,它们分别与原来静止的三个小球A、B、C相碰,相碰后,
在光滑的水平面上以相同的速度运动,它们分别与原来静止的三个小球A、B、C相碰,相碰后, 球继续沿原来的方向运动,
球继续沿原来的方向运动, 球静止,
球静止, 球被反弹回来,这时A、B、C三个被碰小球中动量最大的是 ( )
球被反弹回来,这时A、B、C三个被碰小球中动量最大的是 ( )
A. A球 B. B球 C. C球 D. 无法确定
试题篮
()