高中物理电荷守恒定律综合题

求：（1）m从 A到 D过程中，系统损失了多少机械能？
（2）若 m通过D点时立即撤去磁场，在这以后小车获得的最大速度是多少？

如图所示，在光滑的水平面上有质量为m的小车处于静止状态，车底板光滑绝缘，左右两块金属板M和N竖直固定在车上，它们间的距离为d，分别接电压为U的电源两端，N接电源负极且接地．

(1)现有一可看作质点的带正电荷q、质量为的物块A放置在靠近M板的地方(与M板不接触)如图(甲)所示，释放后，求当物块穿过N板的小孔时刻物块和车速度各是多大？
(2)如图(乙)，若物块从N板的小孔以速度射入静止小车的两板间，求物块在两板电场中的最大电势能和小车达到的最大速度(物块始终不与M板接触)
 

(2)若两小球恰从下边界上的O′点离开电场，则金属板长度L应为多长？并在图示坐标纸上画出两小球在电场中水平方向和竖直方向两个分运动的v-t图象，要求标明坐标值。

如图甲所示，物块A、B的质量分别是m_A=" 4.0kg" 和m_B= 3.0kg，用轻弹簧栓接相连放在光滑的水平地面上，物块B右侧与竖直墙相接触．另有一物块C从t =0时以一定速度向右运动，在t =" 4" s 时与物块A相碰，并立即与A粘在一起不再分开．物块C的v-t 图象如图乙所示．求：
（1）物块C的质量m_C；
（2）墙壁对物块B的弹力在4 s 到12 s 的时间内对B做的功W及对B的冲量I的大小和方向；
（3）B离开墙后的过程中弹簧具有的最大弹性势能E_P．

光滑水平面上一平板车质量为M＝50kg，上面站着质量m＝70kg的人，共同以速度v₀匀速前进，若人相对车以速度v=2m/s向后跑，问人跑动后车的速度改变了多少?

如图，绝缘水平面AB上方，MN左侧存在着水平向右的匀强电场，场强为E＝500v/m,MN和PQ之间存在着方向水平垂直纸面向里的匀强磁场，且边界MN上即无电场，将质量为m₁＝0.02kg，带电量为q₁＝2×10^-4C的表面绝缘的物块a（视作质点）自距离MN为L＝2m的A点由静止释放，物块A向右加速，并与放置在MN边界上质量为m₂＝0.06kg，带电量为q₂＝6×10^-2C表面绝缘的物块b发生没有机械能损失的碰撞，已知二者与水平面间的动磨擦因数均为μ＝0.1，最终发现物块b沿水平面穿出边界PQ后在无场区又运动了2s后停止运动,  (g=10m/s²)，不计两物块间的库仑力，据此求解下列问题

（1）　磁场的磁感应强度大小B。
（2）　物块a再次返回边界MN时的速度大小v。

质量为M=0.4kg的平板静止在光滑的水平面上，如图所示，当t=0时，质量为=0.4kg的小物块A和质量为=0.2kg的小物块B，分别从平板左右两端以相同大小的水平速度=6.0m/s同时冲上平板，当它们相对于平板都停止滑动时，没有相碰。已知A、B两物块与平板的动摩擦因数都是0.2，g取10m/s²，求:

(1)A、B两物体在平板上都停止滑动时平板的速度；
⑵从A、B两物块滑上平板到物块A刚相对于平板静止过程中，A、B及平板组成的系统损失的机械能；
⑶请在下面坐标系中画出平板运动的v—t图象（要写出计算过程）。

(16分)如图所示，一长为L=0.8m不可伸长的轻绳，一端拴着质量为m的小球A，另一端拴于天花板上的O点。现将轻绳水平拉直，并将小球A由静止释放，当小球A运动到最低点时，恰好与放在光滑水平地面上质量为2m的小球B正碰，已知碰撞过程中无机械能损失，碰后A球反弹。以地面为零势能面，重力加速度g="10" m/s²。求：
(1)小球B碰后的速度大小v；
(2)小球A在碰撞过程中损失的机械能与碰前机械能之比。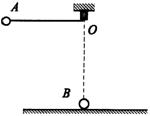

水平固定的两根足够长的平行光滑杆MN、PQ，两者之间的间距为L，两光滑杆上分别穿有一个质量分别为M_A=0.1kg和M_B=0.2kg的小球A、B，两小球之间用一根自然长度也为L的轻质橡皮绳相连接，开始时两小球处于静止状态，轻质橡皮绳处于自然伸长状态，如图（a）所示。现给小球A一沿杆向右的水平瞬时冲量I，以向右为速度正方向，得到A球的速度—时间图象如图(b)所示。（以小球A获得瞬时冲量开始计时，以后的运动中橡皮绳的伸长均不超过其弹性限度。）


（1）求瞬时冲量I的大小；
（2）在图(b)中大致画出B球的速度—时间图象；(不写分析过程直接画图)
（3）若在A球的左侧较远处还有另一质量为M_C=0.1kg小球C，某一时刻给C球4m/s的速度向右匀速运动，它将遇到小球A，并与之结合在一起运动，试定量分析在各种可能的情况下橡皮绳的最大弹性势能。   

如图所示，水平光滑地面上放置有n个完全相同的小车，他们的质量均为m，其中最后一个车右上角上放有质量为M可以看作质点的物块，物块和车之间的动摩擦因数为μ，现在给第一个小车作用向右的瞬时冲量，使其获得速度V₀，设各小车碰撞后立即粘合在一起。运动过程中，物块最终未掉于地面上。求：
①物块M在车上发生相对运动的时间。
②为使物块不掉于地面，每个小车的最小长度L为多大？

（1）测年法是利用衰变规律对古生物进行年代测定的方法。若以横坐标t表示时间，纵坐标m表示任意时刻的质量，为时的质量。下面四幅图中能正确反映衰变规律的是。（填选项前的字母）

A．

B．

C．

D．

（2）如图所示，一个木箱原来静止在光滑水平面上，木箱内粗糙的底板上放着一个小木块。木箱和小木块都具有一定的质量。现使木箱获得一个向右的初速度，则。（填选项前的字母）

A．	小木块和木箱最终都将静止
B．	小木块最终将相对木箱静止，二者一起向右运动
C．	小木块在木箱内壁将始终来回往复碰撞，而木箱一直向右运动
D．	如果小木块与木箱的左壁碰撞后相对木箱静止，则二者将一起向左运动

（共18分）如图所示，在一光滑的长直轨道上，放着若干完全相同的小木块，每个小木块的质量均为m，且体积足够小均能够看成质点，其编号依次为0、1、2、……n……，相邻各木块之间的距离分别记作：。在所有木块都静止的初始条件下，有一个沿轨道方向水平向右的恒力F持续作用在0号小木块上，使其与后面的木块连接发生碰撞，假如所有碰撞都是完全非弹性的（碰后合为一体共速运动）。求：

（1）在0号木块与1号木块碰撞后瞬间，其共同速度的表达式；
（2）若F=10牛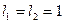，米，那么在2号木块被碰撞后的瞬间，系统的总动能为多少？
（3）在F=10牛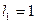，米的前提下，为了保持正在运动的物块系统在每次碰撞之前的瞬间其总动能都为一个恒定的数值，那么我们应该设计第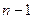号和第n号木块之间距离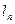为多少米？

总质量为M的气球以2m/s的速度匀速上升，在某高度处，从气球上落下质量为M/5的物体，不计空气阻力，物体落地时的速率为14m/s，则此时气球的速率为多大？

如图所示，在光滑的水平面上固定有左、右两竖直挡板，挡板间距离足够长，有一质量为M，长为L的长木板靠在左侧挡板处，另有一质量为m的小物块（可视为质点），放置在长木板的左端，已知小物块与长木板间的动摩擦因数为μ，且M>m．现使小物块和长木板以共同速度v₀向右运动，设长木板与左、右挡板的碰撞中无机械能损失．试求：

（1）将要发生第二次碰撞时，若小物块仍未从长木板上落下，则它应距长木板左端多远？
（2）为使小物块不从长木板上落下，板长L应满足什
么条件？
（3）若满足（2）中条件，且M=2kg，m=1kg，v₀=10m/s，试计算整个系统在刚发生第四次碰撞前损失的机械能．